Discretization, Explained: A Visual Guide with Code Examples for Beginners
DATA PREPROCESSING
6 fun ways to categorize numbers into bins!
Most machine learning model requires the data to be numerical — all object or categorical data has to be in numerical format first. But, actually, there are times when categorical data comes in handy (it’s more useful to us human than to the machines most of the time). Discretization (or binning) does exactly that — converting numerical data into categorical ones!
Depending on your goal, there are numerous way to categorize your data. Here, we’ll use a simple dataset to show through six different binning methods. From equal-width to clustering-based approaches, we’ll sweep those numerical values into some categorical bins!

What is Discretization?
Discretization, also known as binning, is the process of transforming continuous numerical variables into discrete categorical features. It involves dividing the range of a continuous variable into intervals (bins) and assigning data points to these bins based on their values.
Why Do We Need Binning?
- Handling Outliers: Binning can reduce the impact of outliers without removing data points.
- Improving Model Performance: Some algorithms perform better with categorical inputs (such as Bernoulli Naive Bayes).
- Simplifying Visualization: Binned data can be easier to visualize and interpret.
- Reducing Overfitting: It can prevent models from fitting to noise in high-precision data.
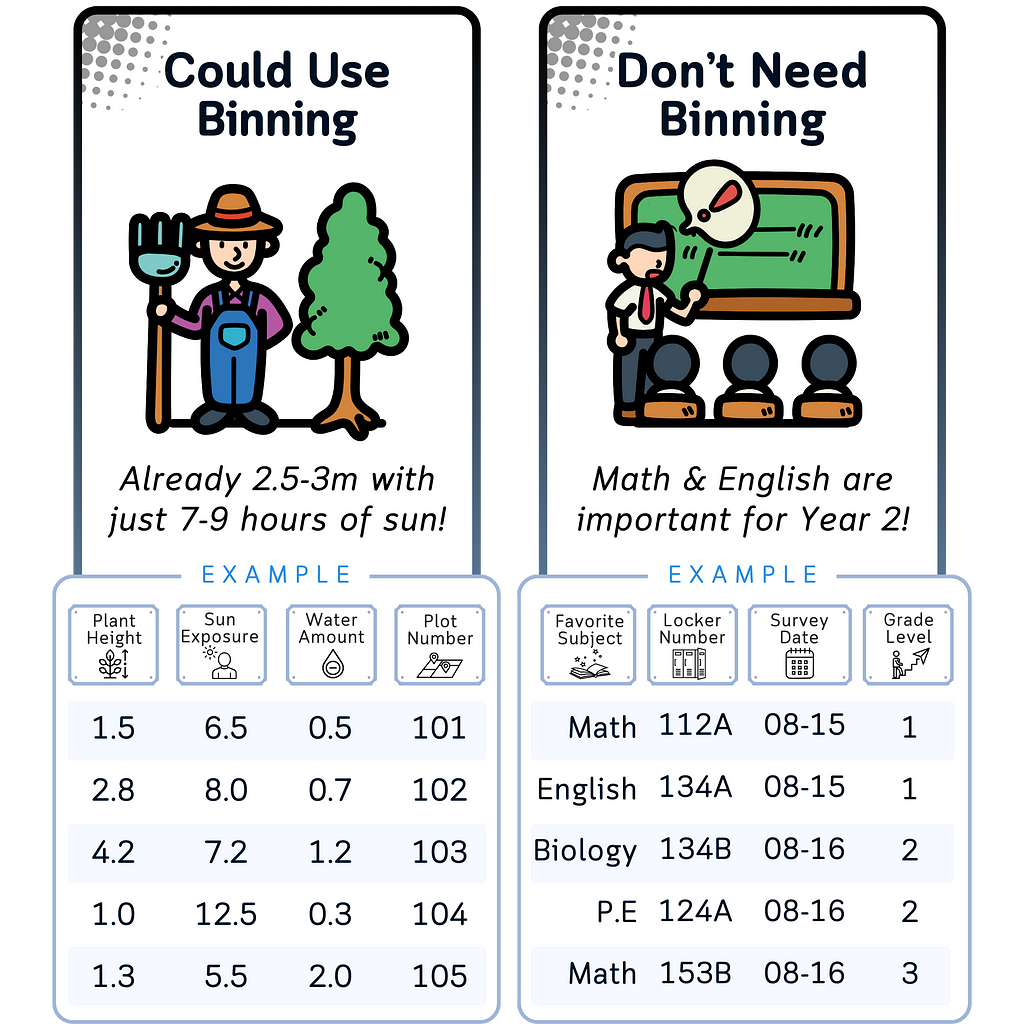
Which Data Needs Binning?
Data That Often Benefits from Binning:
- Continuous variables with wide ranges: Variables with a large spread of values can often benefit from grouping.
- Skewed distributions: Binning can help normalize heavily skewed data.
- Variables with outliers: Binning can handle the effect of extreme values.
- High-cardinality numerical data: Variables with many unique values can be simplified through binning.
Data That Usually Doesn’t Need Binning:
- Already categorical data: Variables that are already in discrete categories don’t need further binning.
- Discrete numerical data with few unique values: If a variable only has a small number of possible values, binning might not provide additional benefit.
- Numeric IDs or codes: These are meant to be unique identifiers, not for analysis.
- Time series data: While you can bin time series data, it often requires specialized techniques and careful consideration, but less common overall.
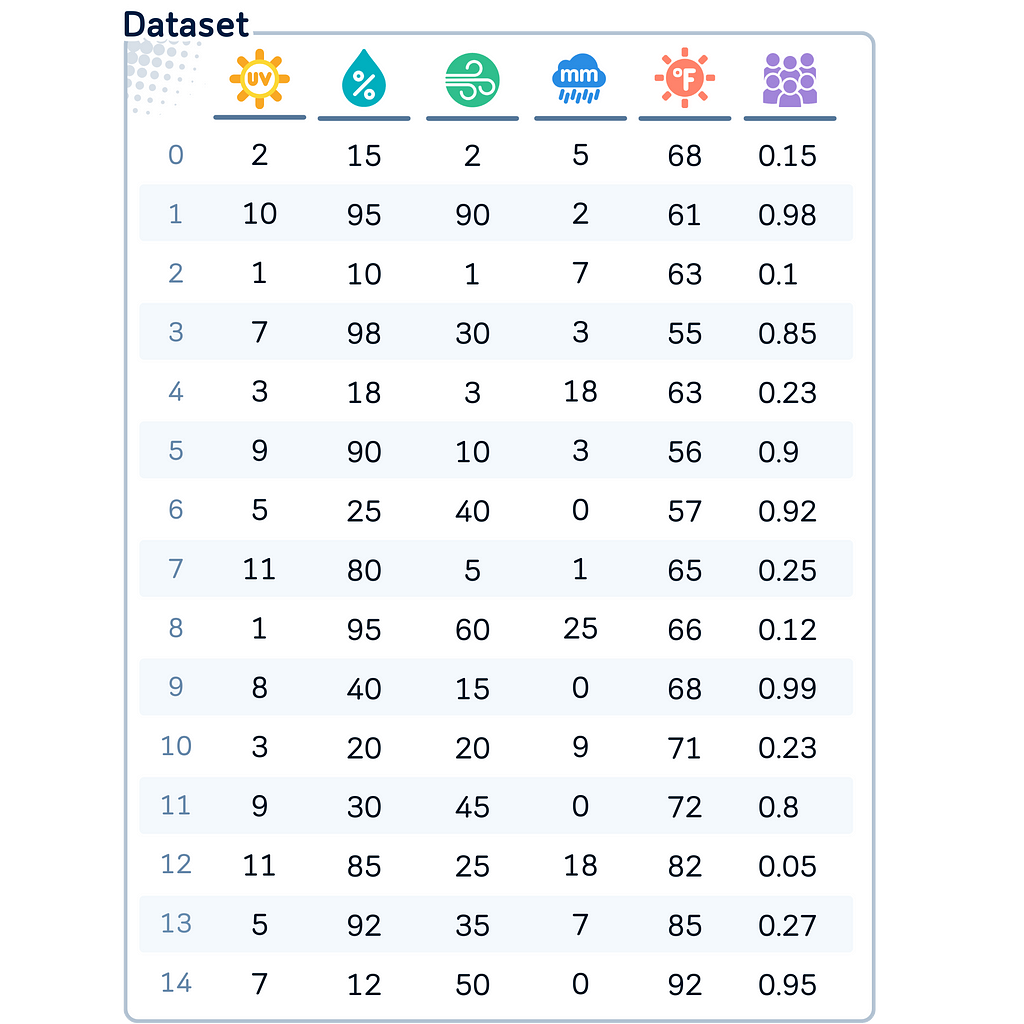
The Dataset
To demonstrate these binning techniques, we’ll be using this artificial dataset. Say, this is the weather condition in some golf course, collected on 15 different days.
import pandas as pd
import numpy as np
# Create the dataset as a dictionary
data = {
'UVIndex': [2, 10, 1, 7, 3, 9, 5, 11, 1, 8, 3, 9, 11, 5, 7],
'Humidity': [15, 95, 10, 98, 18, 90, 25, 80, 95, 40, 20, 30, 85, 92, 12],
'WindSpeed': [2, 90, 1, 30, 3, 10, 40, 5, 60, 15, 20, 45, 25, 35, 50],
'RainfallAmount': [5,2,7,3,18,3,0,1,25,0,9,0,18,7,0],
'Temperature': [68, 60, 63, 55, 50, 56, 57, 65, 66, 68, 71, 72, 79, 83, 81],
'Crowdedness': [0.15, 0.98, 0.1, 0.85, 0.2, 0.9, 0.92, 0.25, 0.12, 0.99, 0.2, 0.8, 0.05, 0.3, 0.95]
}
# Create a DataFrame from the dictionary
df = pd.DataFrame(data)
Using this dataset, let’s see how various binning techniques can be applied to our columns!
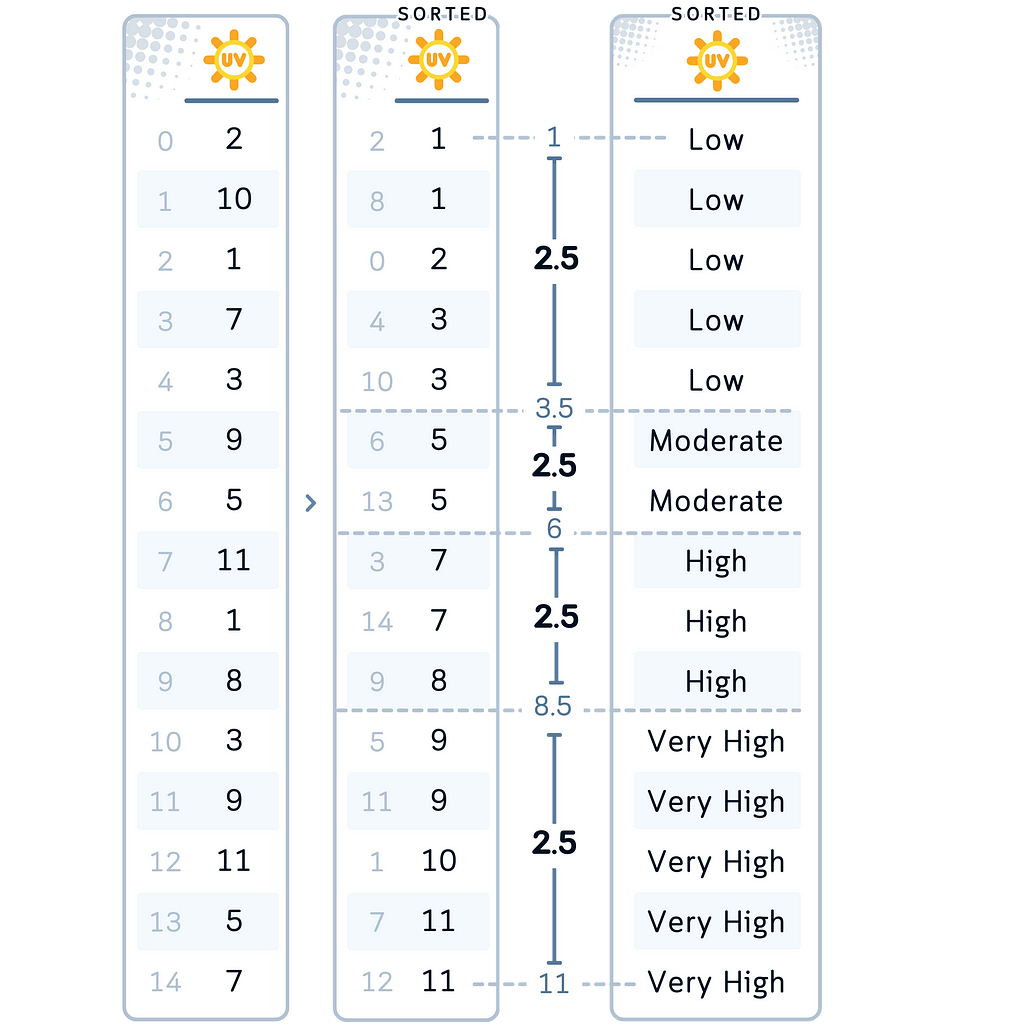
Method 1: Equal-Width Binning
Equal-width binning divides the range of a variable into a specified number of intervals, all with the same width.
Common Data Type: This method works well for data with a roughly uniform distribution and when the minimum and maximum values are meaningful.
In our Case: Let’s apply equal-width binning to our UV Index variable. We’ll create four bins: Low, Moderate, High, and Very High. We chose this method for UV Index because it gives us a clear, intuitive division of the index range, which could be useful for understanding how different index ranges affect golfing decisions.
# 1. Equal-Width Binning for UVIndex
df['UVIndexBinned'] = pd.cut(df['UVIndex'], bins=4,
labels=['Low', 'Moderate', 'High', 'Very High'])
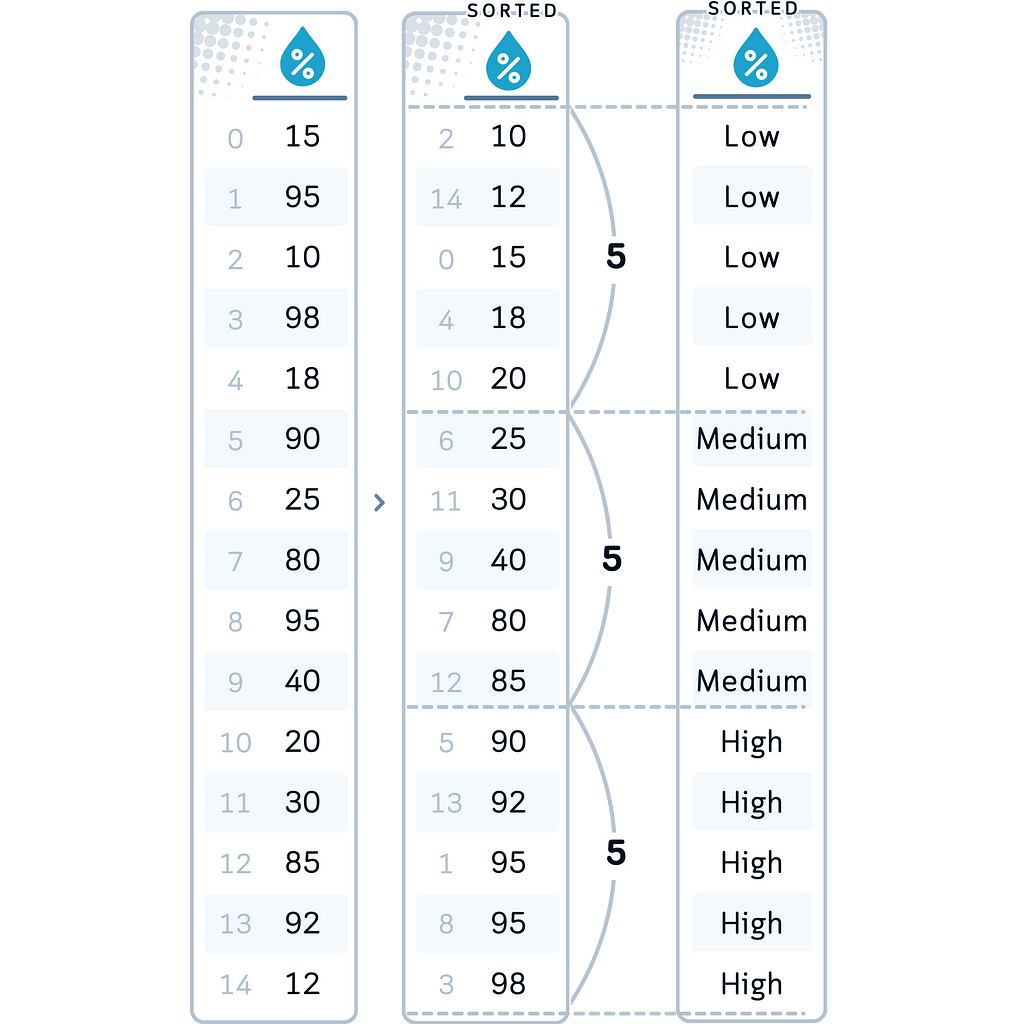
Method 2: Equal-Frequency Binning (Quantile Binning)
Equal-frequency binning creates bins that contain approximately the same number of observations.
Common Data Type: This method is particularly useful for skewed data or when you want to make sure a balanced representation across categories.
In our Case: Let’s apply equal-frequency binning to our Humidity variable, creating three bins: Low, Medium, and High. We chose this method for Humidity because it ensures we have an equal number of observations in each category, which can be helpful if humidity values are not evenly distributed across their range.
# 2. Equal-Frequency Binning for Humidity
df['HumidityBinned'] = pd.qcut(df['Humidity'], q=3,
labels=['Low', 'Medium', 'High'])
Method 3: Custom Binning
Custom binning allows you to define your own bin edges based on domain knowledge or specific requirements.
Common Data Type: This method is ideal when you have specific thresholds that are meaningful in your domain or when you want to focus on particular ranges of values.
In our Case: Let’s apply custom binning to our Rainfall Amount. We chose this method for this column because there are standardized categories for rain (such as described in this site) that are more meaningful than arbitrary divisions.
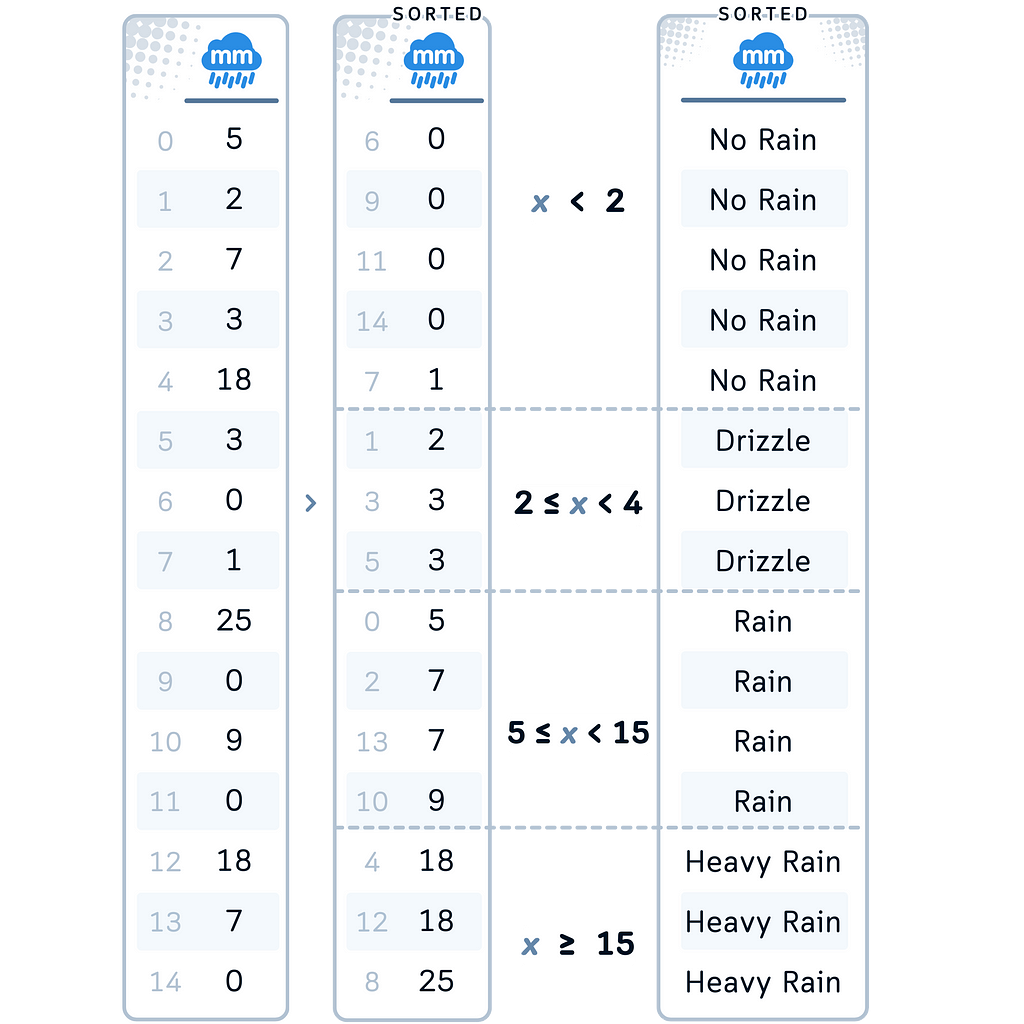
# 3. Custom Binning for RainfallAmount
df['RainfallAmountBinned'] = pd.cut(df['RainfallAmount'], bins=[-np.inf, 2, 4, 12, np.inf],
labels=['No Rain', 'Drizzle', 'Rain', 'Heavy Rain'])
Method 4: Logarithmic Binning
Logarithmic binning creates bins that grow exponentially in size. The method basically applies log transformation first then performs equal-width binning.
Common Data Type: This method is particularly useful for data that spans several orders of magnitude or follows a power law distribution.
In our Case: Let’s apply logarithmic binning to our Wind Speed variable. We chose this method for Wind Speed because the effect of wind on a golf ball’s trajectory might not be linear. A change from 0 to 5 mph might be more significant than a change from 20 to 25 mph.
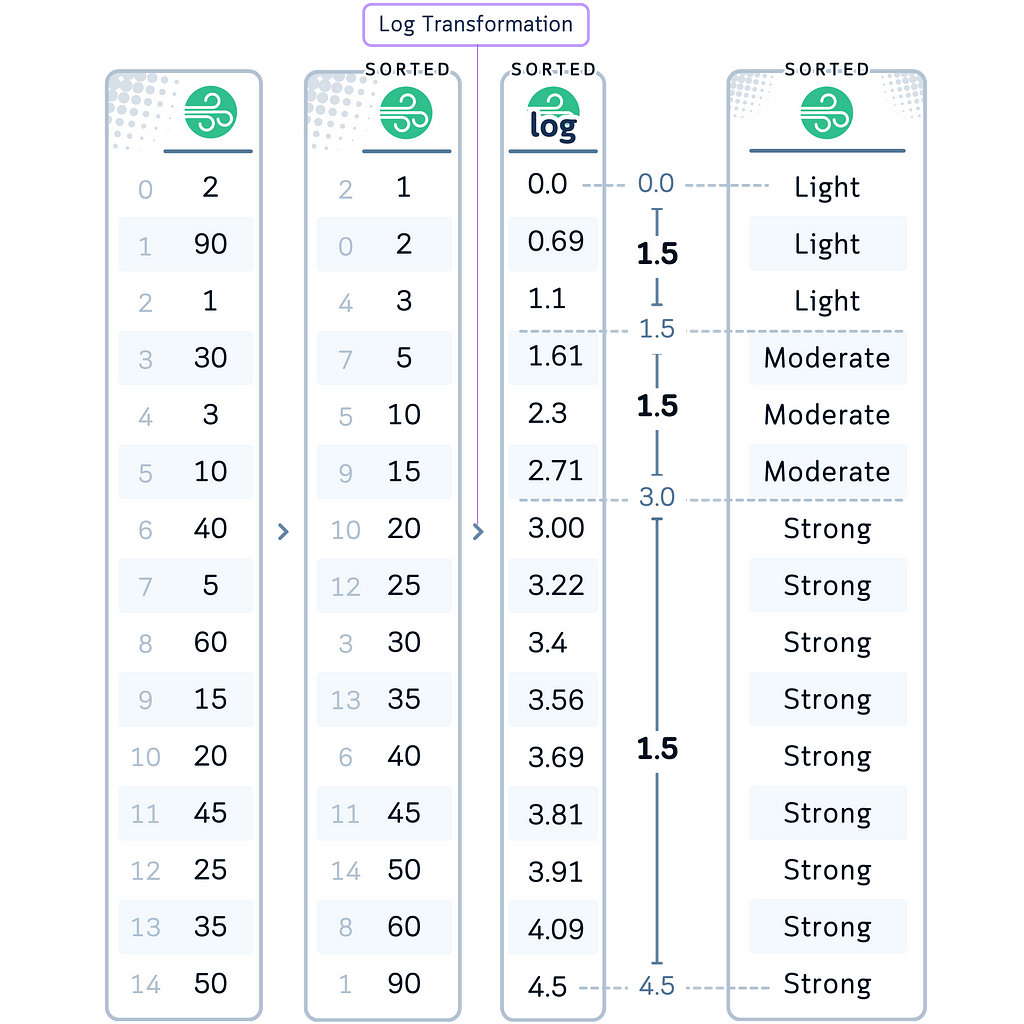
# 4. Logarithmic Binning for WindSpeed
df['WindSpeedBinned'] = pd.cut(np.log1p(df['WindSpeed']), bins=3,
labels=['Light', 'Moderate', 'Strong'])
Method 5: Standard Deviation-based Binning
Standard Deviation based binning creates bins based on the number of standard deviations away from the mean. This approach is useful when working with normally distributed data or when you want to bin data based on how far values deviate from the central tendency.
Variations: The exact number of standard deviations used for binning can be adjusted based on the specific needs of the analysis. The number of bins is typically odd (to have a central bin). Some implementations might use unequal bin widths, with narrower bins near the mean and wider bins in the tails.
Common Data Type: This method is well-suited for data that follows a normal distribution or when you want to identify outliers and understand the spread of your data. May not be suitable for highly skewed distributions.
In our Case: Let’s apply this binning method scaling to our Temperature variable. We chose this method for Temperature because it allows us to categorize temperatures based on how they deviate from the average, which can be particularly useful in understanding weather patterns or climate trends.
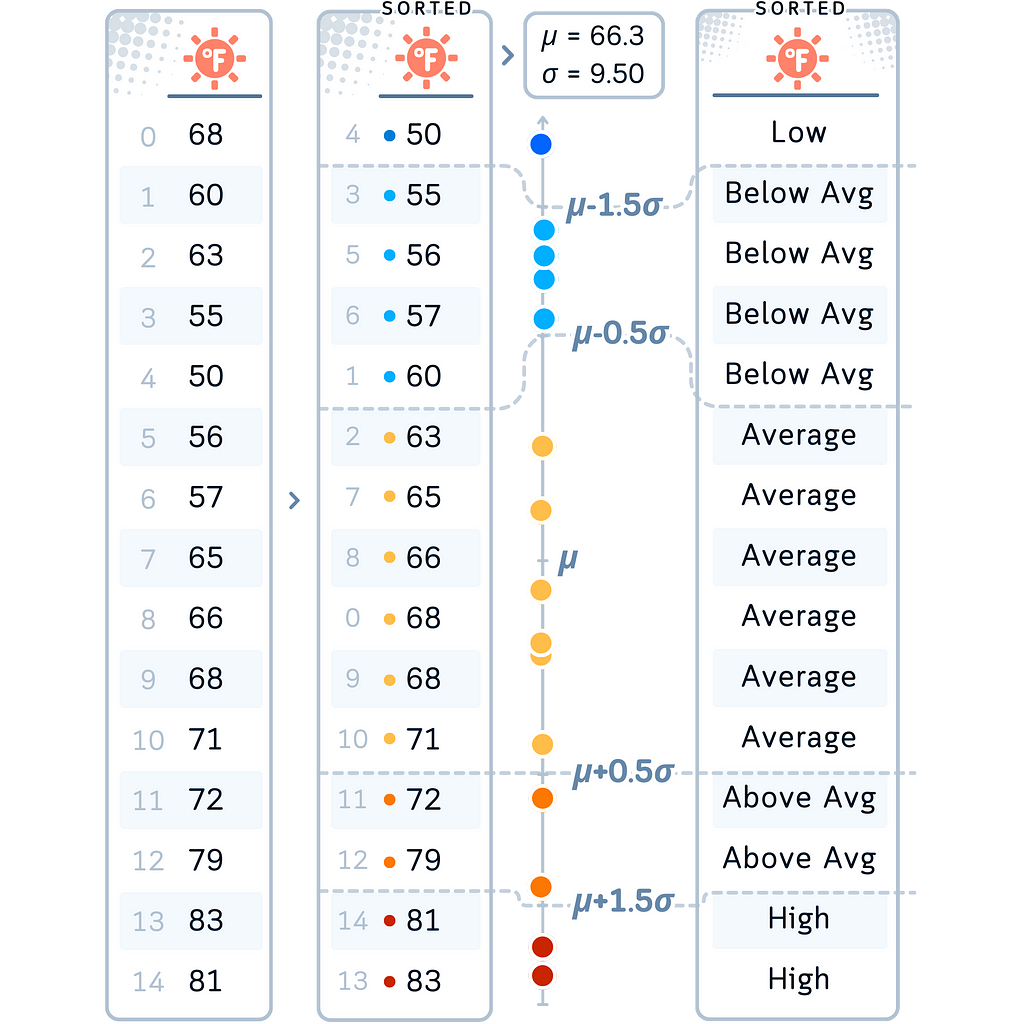
# 5. Standard Deviation-Based Binning for Temperature
mean_temp, std_dev = df['Temperature'].mean(), df['Temperature'].std()
bin_edges = [
float('-inf'), # Ensure all values are captured
mean_temp - 2.5 * std_dev,
mean_temp - 1.5 * std_dev,
mean_temp - 0.5 * std_dev,
mean_temp + 0.5 * std_dev,
mean_temp + 1.5 * std_dev,
mean_temp + 2.5 * std_dev,
float('inf') # Ensure all values are captured
]
df['TemperatureBinned'] = pd.cut(df['Temperature'], bins=bin_edges,
labels=['Very Low', 'Low', 'Below Avg', 'Average','Above Avg', 'High', 'Very High'])
Method 6: K Means Binning
K-Means binning uses the K-Means clustering algorithm to create bins. It groups data points into clusters based on how similar the data points are to each other, with each cluster becoming a bin.
Common Data Type: This method is great for finding groups in data that might not be obvious at first. It works well with data that has one peak or several peaks, and it can adjust to the way the data is organized.
In our Case: Let’s apply K-Means binning to our Crowdedness variable. We chose this method for Crowdedness because it might reveal natural groupings in how busy the golf course gets, which could be influenced by various factors not captured by simple threshold-based binning.
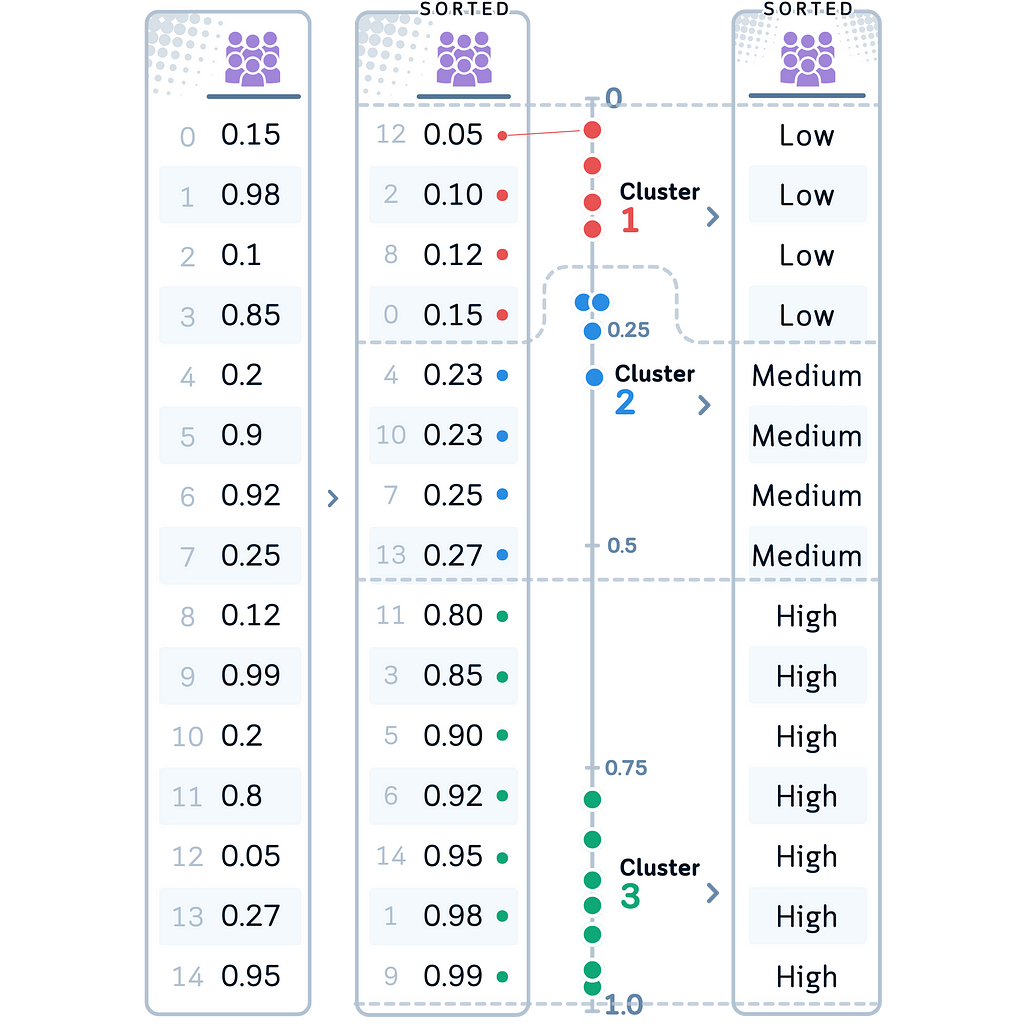
# 6. K-Means Binning for Crowdedness
kmeans = KMeans(n_clusters=3, random_state=42).fit(df[['Crowdedness']])
df['CrowdednessBinned'] = pd.Categorical.from_codes(kmeans.labels_, categories=['Low', 'Medium', 'High'])
Conclusion
We tried six different ways to ‘discretize’ the numbers in our golf data. So, the final dataset now looks like this:
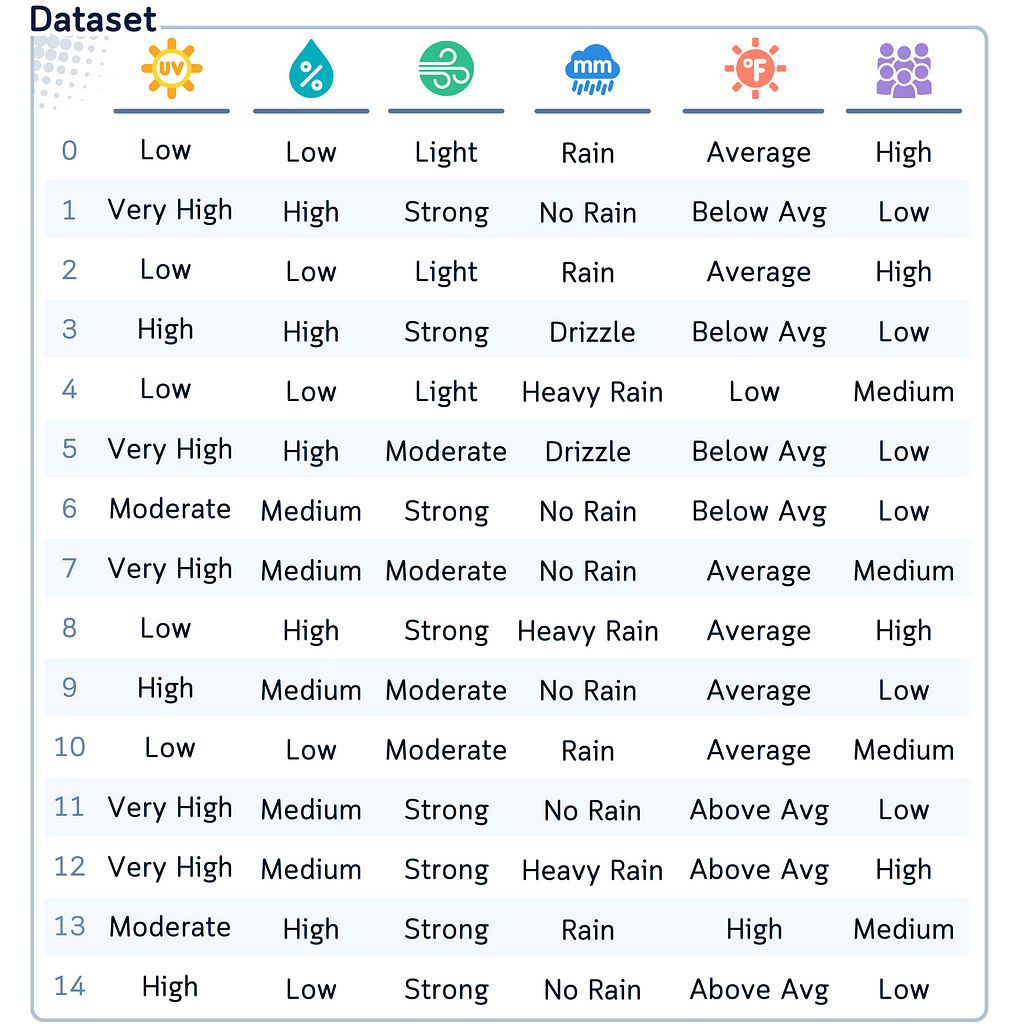
# Print only the binned columns
binned_columns = [col for col in df.columns if col.endswith('Binned')]
print(df[binned_columns])
Let’s review how each binning technique transformed our weather data:
- Equal-Width Binning (UVIndex): Divided our UV Index scale into four equal ranges, categorizing exposure levels from ‘Low’ to ‘Very High’. This gives a straightforward interpretation of UV intensity.
- Equal-Frequency Binning (Humidity): Sorted our Humidity readings into ‘Low’, ‘Medium’, and ‘High’ categories, each containing an equal number of data points. This approach makes sure a balanced representation across humidity levels.
- Logarithmic Binning (WindSpeed): Applied to our Wind Speed data, this method accounts for the non-linear impact of wind on weather conditions, categorizing speeds as ‘Light’, ‘Moderate’, or ‘Strong’.
- Custom Binning (RainfallAmount): Used domain knowledge to classify rainfall into meaningful categories from ‘No Rain’ to ‘Heavy Rain’. This method directly translates measurements into practical weather descriptions.
- Standard Deviation-Based Binning (Temperature): Segmented our Temperature data based on its distribution, ranging from ‘Very Low’ to ‘Very High’. This approach highlights how temperatures deviate from the average.
- K-Means Binning (Crowdedness): Showed natural groupings in our Crowdedness data, potentially showing patterns.
It’s important to avoid applying binning techniques with no thought. The nature of each variable and your analytical goals are always varied and it’s good to keep that in mind when selecting a binning method. In many cases, trying out multiple techniques and comparing their outcomes can provide the most insights into your data!
⚠️ The Risks of Binning
While performing binning sounds easy, it comes with its own risks:
- Information Loss: When you bin data, you’re essentially smoothing over the details. This can be great for spotting trends, but you might miss out on subtle patterns or relationships within the bins.
- Arbitrary Boundaries: The choice of bin edges can sometimes feel like more art than science. A slight shift in these boundaries can lead to different interpretations of your data.
- Model Impact: Some models, particularly tree-based ones like Decision Tree, might actually perform worse with binned data. They’re pretty good at finding their own ‘bins’, so to speak.
- False Sense of Security: Binning can make your data look neater and more manageable, but the underlying complexity is still there. Just hidden.
- Difficulty in Interpretation: While binning can simplify analysis, it can also make it harder to interpret the magnitude of effects. “High” temperature could mean very different things in different contexts.
So, what’s a data scientist to do? Here’s my advice:
- Always keep a copy of your unbinned data. You might need to go back to it.
- Try different binning strategies and compare the results. Don’t settle for the first method you try.
- Look up if there’s already a standard way in the domain of the dataset to categorize the data (like our “Rainfall Amount” example above.)
🌟 Discretization Summarized
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
# Create the dataset
data = {
'UVIndex': [2, 10, 1, 7, 3, 9, 5, 11, 1, 8, 3, 9, 11, 5, 7],
'Humidity': [15, 95, 10, 98, 18, 90, 25, 80, 95, 40, 20, 30, 85, 92, 12],
'WindSpeed': [2, 90, 1, 30, 3, 10, 40, 5, 60, 15, 20, 45, 25, 35, 50],
'RainfallAmount': [5,2,7,3,18,3,0,1,25,0,9,0,18,7,0],
'Temperature': [68, 60, 63, 55, 50, 56, 57, 65, 66, 68, 71, 72, 79, 83, 81],
'Crowdedness': [0.15, 0.98, 0.1, 0.85, 0.2, 0.9, 0.92, 0.25, 0.12, 0.99, 0.2, 0.8, 0.05, 0.3, 0.95]
}
# Create a DataFrame from the dictionary
df = pd.DataFrame(data)
# 1. Equal-Width Binning for UVIndex
df['UVIndexBinned'] = pd.cut(df['UVIndex'], bins=4,
labels=['Low', 'Moderate', 'High', 'Very High'])
# 2. Equal-Frequency Binning for Humidity
df['HumidityBinned'] = pd.qcut(df['Humidity'], q=3,
labels=['Low', 'Medium', 'High'])
# 3. Custom Binning for RainfallAmount
df['RainfallAmountBinned'] = pd.cut(df['RainfallAmount'], bins=[-np.inf, 2, 4, 12, np.inf],
labels=['No Rain', 'Drizzle', 'Rain', 'Heavy Rain'])
# 4. Logarithmic Binning for WindSpeed
df['WindSpeedBinned'] = pd.cut(np.log1p(df['WindSpeed']), bins=3,
labels=['Light', 'Moderate', 'Strong'])
# 5. Standard Deviation-Based Binning for Temperature
mean_temp, std_dev = df['Temperature'].mean(), df['Temperature'].std()
bin_edges = [
float('-inf'), # Ensure all values are captured
mean_temp - 2.5 * std_dev,
mean_temp - 1.5 * std_dev,
mean_temp - 0.5 * std_dev,
mean_temp + 0.5 * std_dev,
mean_temp + 1.5 * std_dev,
mean_temp + 2.5 * std_dev,
float('inf') # Ensure all values are captured
]
df['TemperatureBinned'] = pd.cut(df['Temperature'], bins=bin_edges,
labels=['Very Low', 'Low', 'Below Avg', 'Average','Above Avg', 'High', 'Very High'])
# 6. KMeans Binning for Crowdedness
kmeans = KMeans(n_clusters=3, random_state=42).fit(df[['Crowdedness']])
df['CrowdednessBinned'] = pd.Categorical.from_codes(kmeans.labels_, categories=['Low', 'Medium', 'High'])
# Print only the binned columns
binned_columns = [col for col in df.columns if col.endswith('Binned')]
print(df[binned_columns])
Technical Environment
This article uses Python 3.7 and scikit-learn 1.5. While the concepts discussed are generally applicable, specific code implementations may vary slightly with different versions.
About the Illustrations
Unless otherwise noted, all images are created by the author, incorporating licensed design elements from Canva Pro.
Discretization, Explained: A Visual Guide with Code Examples for Beginners was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Datascience in Towards Data Science on Medium https://ift.tt/5payCnd
via IFTTT




