Datascience in Towards Data Science on Medium,

How to Perform A/B Testing with Hypothesis Testing in Python: A Comprehensive Guide

10/13/2024 Jesus Santana

A Step-by-Step Guide to Making Data-Driven Decisions with Practical Python Examples

Have you ever wondered if a change to your website or marketing strategy truly makes a difference? 🤔 In this guide, I’ll show you how to use hypothesis testing to make data-driven decisions with confidence.

In data analytics, hypothesis testing is frequently used when running A/B tests to compare two versions of a marketing campaign, webpage design, or product feature to make data-driven decisions.

What You’ll Learn 🧐

• The process of hypothesis testing
• Different types of tests
• Understanding p-values
• Interpreting the results of a hypothesis test

1. Understanding Hypothesis Testing 🎯

What Is Hypothesis Testing?

Hypothesis testing is a way to decide whether there is enough evidence in a sample of data to support a particular belief about the population. In simple terms, it’s a method to test if a change you made has a real effect or if any difference is just due to chance.

Key Concepts:

• Population Parameter: A value that represents a characteristic of the entire population (e.g., the true conversion rate of a website).
• Sample Statistic: A value calculated from a sample, used to estimate the population parameter (e.g., the conversion rate from a sample of visitors).
• Null Hypothesis (H0​): The default assumption. It often states that there is no effect or no difference.
• Alternative Hypothesis (H1​): Contradicts the null hypothesis. It represents the outcome you’re testing for.

⚠️ Your goal will be to negate the null hypothesis and therefore accept the alternative hypothesis ⚠️

Types of Tests

Depending on your data and what you’re testing, you can choose from several statistical tests. Here’s a quick overview:

1. Z-test

• Purpose: Used to see if there is a significant difference between sample and population means, or between means or proportions of two samples, when the sample size is large.
• When to Use:
• Large sample size (n≥30)
• Data is approximately normally distributed

Example: Checking if the average time users spend on your website is different from the industry average.

Types of Z-tests:

One-Sample Z-test for Means: Tests whether the sample mean is significantly different from a known population mean.

Two-Sample Z-test for Means: Compares the means of two independent samples.

Z-test for Proportions: Tests hypotheses about population proportions, often used when dealing with categorical data and large sample sizes.

2. T-test

• Purpose: Used to determine if there is a significant difference between sample means when the sample size is small.
• When to Use:
• Small sample size (n< 30)
• Population variance is unknown
• Data is approximately normally distributed

Example: Comparing average sales before and after a marketing campaign when you have a small dataset.

Types of T-tests:

One-Sample T-test: Tests whether the sample mean is significantly different from a known or hypothesized population mean.

Independent Two-Sample T-test: Compares the means of two independent samples.

Paired Sample T-test: Compares means from the same group at different times (e.g., before and after treatment).

3. Chi-Square Test

• Purpose: Used for testing relationships between categorical variables.
• When to Use:
• Data is in categories (like yes/no, male/female)
• Testing for independence or goodness-of-fit

Example: Determining if customer satisfaction is related to the type of product purchased.

Types of Chi-Square Tests:

Chi-Square Test for Independence: Determines whether there is an association between two categorical variables.

Chi-Square Goodness-of-Fit Test: Determines whether sample data matches a population distribution.

4. ANOVA (Analysis of Variance)

• Purpose: Used to compare the means of three or more groups.
• When to Use:
• Comparing more than two groups
• Data is numerical and normally distributed

Example: Comparing average sales across different regions.

2. The Hypothesis Testing Process 📝

To perform a hypothesis test, follow these seven steps:

1. State the Hypotheses
2. Choose the Significance Level (α)
3. Collect and Summarize the Data
4. Select the Appropriate Test and Check Assumptions
5. Calculate the Test Statistic
6. Determine the p-value
7. Make a Decision and Interpret the Results

Let’s go through each step with a practical example

3. Practical Example: A/B Testing in Marketing 📊

Scenario:

Imagine you want to know if a new version of your website (Version B) leads to a higher conversion rate than your current website (Version A). Let’s find out!

Which Test Should You Use and Why?

You’re comparing the conversion rates (proportions) of two versions of a website.

Your Goal: To determine whether Version B has a higher conversion rate than Version A.

Characteristics of Your Data:

• Type of Data: Categorical (converted vs. not converted)
• Sample Size: Large for both versions (nA=nB=1,000)
• Known Parameters: Population variances are not known
• Number of Groups: Two independent groups
• Study Design: Samples are independent; visitors are randomly assigned to each version

Given these characteristics, the Z-test for Proportions is the right choice because:

• You’re comparing proportions between two independent samples
• The sample sizes are large
• The data is categorical.

Step 1: State the Hypotheses 🧐

• Null Hypothesis (H0): The conversion rate of Version B is less than or equal to that of Version A ❌.

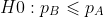
• Alternative Hypothesis (H1​): The conversion rate of Version B is greater than that of Version A ✅.

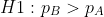
Explanation:

• You’re testing if Version B performs better than Version A.
• The null hypothesis assumes there’s no improvement or that Version B is worse.
• The alternative hypothesis is what you’re hoping to find evidence for — that Version B is better.

Step 2: Choose the Significance Level (α) 🎯

Select α significance level, which is the probability of rejecting the null hypothesis when it’s actually true (committing a Type I error).

• Common choices: 0.05 (5%), 0.01 (1%)
• For our test: Let’s use α=0.05.

Explanation:

• A 5% significance level means you’re willing to accept a 5% chance of mistakenly rejecting the null hypothesis.
• The choice depends on how much risk you’re willing to take.

Step 3: Collect and Summarize the Data 📈

Version A (Current Website):

• Sample size (nA​) = 1,000 visitors
• Number of conversions (xA​) = 80
• Conversion rate (pA​) = 80/1000=0.08(8%)

Version B (New Website):

• Sample size (nB) = 1,000 visitors
• Number of conversions (xB​) = 95
• Conversion rate (pB​) = 95/1000=0.095(9.5%)

Step 4: Calculate the Test Statistic 🧮

Calculate the Pooled Proportion (p)

Since you’re assuming the proportions are equal under H0:

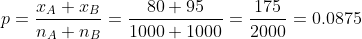
Explanation:

• The pooled proportion represents the overall conversion rate assuming no difference between versions.
• It provides a common proportion for calculating the standard error under H0​.

Calculate the Standard Error (SE)

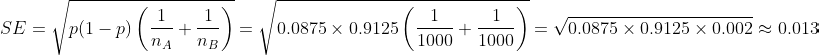
Explanation:

• The standard error measures the variability we’d expect from random sampling.

Calculate the Z-Score

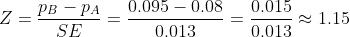
Explanation:

• The Z-score measures how many standard errors the observed difference between the two sample proportions is away from zero (the expected difference under H0​).
• Z-score: 1.15
• Expected Difference Under H0​: If H0​ is true, we expect no difference, so this is 0

Question:

• Is being 1.15 standard errors above the expected difference enough to consider the increase significant?

Step 5: Determine the p-value 📊

Understanding the p-value

The p-value is the probability of observing a Z-score as extreme as the one calculated (or more extreme) if the null hypothesis H0​ is true.

In our example, the p-value is the probability of getting a Z-score of 1.15 or higher if there is actually no difference between the versions.

For a right-tailed test (since H1: pB>pA), the p-value is:

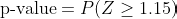
Calculating the p-value:

Using a standard normal distribution table or calculator:

• p-value=1−P(Z≤1.15)≈1−0.8823=0.12

Explanation:

• There’s an 12% chance of getting a Z-score of 1.15 or higher if H0 is true.
• This means the observed difference could easily happen by chance.

Important Note: We won’t dive into the mathematical details of calculating p-values in this tutorial. Instead, we’ll use Python’s statistical libraries to compute them for you or refer to standard probability distribution tables.

Step 6: Make a Decision and Interpret the Results 🧐

To make a decision, we have to compare our p-value and our α.

Why Compare p-value to Significance Level (α)?

• Significance Level (α): The threshold we set for deciding whether an observed result is statistically significant. Commonly set at 5% (0.05).
• If p-value ≤ α : Reject H0​; the result is statistically significant.
• If p-value > α: Fail to reject H0; not enough evidence to conclude a significant effect.

Decision:

• p-value: 0.12
• Significance Level (α): 0.05

Since p-value > α, we fail to reject the null hypothesis.

Interpretation:

• There’s not enough evidence to say that Version B is better than Version A at the 5% significance level.
• The observed increase might just be due to random chance.
• 12% > 5% there is 12% of chance to observe Z>1,15 under the H0 (even if actually there is no difference between the 2 versions).
• Imagine Repeating the Experiment Many Times: If there is truly no difference between Version A and Version B, and you repeat the experiment many times, about 12% of the time, you’d observe a difference as big as 1.5 (or more) just by chance.

Quick Python Tutorial: A/B Testing in Action 🐍

Let’s bring everything we’ve learned to life with a practical example using Python! Our imaginary company called TechGear, wants to test a new feature on their website.

Scenario:

TechGear is an online retailer specializing in tech gadgets. They want to know if adding a new recommendation engine (Version B) increases the purchase rate compared to their current website (Version A).

Step 1: Import Libraries 📚

First, you’ll need to import the necessary Python libraries.

import numpy as np
import pandas as pd
from statsmodels.stats.proportion import proportions_ztest
import matplotlib.pyplot as plt
import seaborn as sns

Step 2: Generate Synthetic Data 🎲

We’ll create a dataset that simulates user behavior on both versions of the website.

# Set the random seed for reproducibility
np.random.seed(42)

# Define sample sizes
n_A = 1000  # Number of visitors in Version A
n_B = 1000  # Number of visitors in Version B

# Define conversion rates
p_A = 0.08   # 8% conversion rate for Version A
p_B = 0.095  # 9.5% conversion rate for Version B

# Generate conversions (1 = purchase, 0 = no purchase)
conversions_A = np.random.binomial(1, p_A, n_A)
conversions_B = np.random.binomial(1, p_B, n_B)

# Create DataFrames
data_A = pd.DataFrame({'version': 'A', 'converted': conversions_A})
data_B = pd.DataFrame({'version': 'B', 'converted': conversions_B})

# Combine data
data = pd.concat([data_A, data_B]).reset_index(drop=True)

Step 3: Summarize the Data 📊

Let’s see how our data looks.

# Calculate the number of conversions and total observations for each version
summary = data.groupby('version')['converted'].agg(['sum', 'count'])
summary.columns = ['conversions', 'total']
print(summary)

Step 4: Perform the Z-test 🧪

We’ll use the proportions_ztest function to perform the hypothesis test.

# Number of successes (conversions) and number of trials (visitors)
conversions = [summary.loc['A', 'conversions'], summary.loc['B', 'conversions']]
nobs = [summary.loc['A', 'total'], summary.loc['B', 'total']]

# Perform the z-test
stat, p_value = proportions_ztest(count=conversions, nobs=nobs, alternative='smaller')

print(f"Z-statistic: {stat:.4f}")
print(f"P-value: {p_value:.4f}")

Explanation:

• Z-statistic: Tells us how many standard deviations our observed difference is from the null hypothesis.
• P-value: The probability of observing such a result if the null hypothesis is true.

Step 5: Interpret the Results 🧐

Let’s interpret the output.

alpha = 0.05  # Significance level

if p_value < alpha:
    print("We reject the null hypothesis. Version B has a higher conversion rate! 🎉")
else:
    print("We fail to reject the null hypothesis. No significant difference detected. 🤔")

• If you rejected H0​: The new recommendation engine is effective! You might consider rolling it out to all users.
• If you failed to reject H0​: The new feature didn’t make a significant impact. You may want to test other ideas.

Additional Notes 📝

• Randomness: Since we’re generating random data, results may vary each time you run the code.
• Repeat Testing: In real-world scenarios, consider running the test with more users or over a longer period to gather more data.

Congratulations! You’ve just performed an A/B test using Python. 🎉

Key Points to Remember 🍀

• Hypothesis Testing Basics: State the Null Hypothesis (H0) and the Alternative Hypothesis (H1).
• Goal: Determine if there’s enough evidence to reject H0​.
• Types of Tests: Choose the appropriate statistical test based on data type and sample size.
• Hypothesis Testing Steps:

1. State the Hypotheses
2. Choose Significance Level (α\alphaα)
3. Collect and Summarize Data
4. Select the Appropriate Test
5. Calculate the Test Statistic
6. Determine the p-value
7. Make a Decision

• Set Clear Objectives: Know exactly what you’re testing and why.
• Randomize Assignments: Randomly assign users to control and test groups to avoid bias.
• Use Sufficient Sample Size: Larger samples yield more reliable results.
• Control Variables: Keep other factors constant to isolate the effect.
• Run the Test Long Enough: Ensure the test duration captures typical user behavior.
• Consider Practical Impact: Evaluate if the detected difference is meaningful for your business.
• Communicate Clearly: Present results in a straightforward way for stakeholders.
• Iterate and Learn: Use findings to inform future tests and improvements.

You made it to the end — congrats! 🎉 I hope you enjoyed this article. If you found it helpful, please consider leaving a like and following me. I will regularly write about demystifying machine learning algorithms, clarifying statistics concepts, and sharing insights on deploying ML projects into production.

---

How to Perform A/B Testing with Hypothesis Testing in Python: A Comprehensive Guide 🚀 was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

from Datascience in Towards Data Science on Medium https://ift.tt/1mGkh9Q
via IFTTT