Recursion — Data Structures & Algorithms for Data Scientists
Recursion — Data Structures & Algorithms for Data Scientists
Recursion, recursion, recursion, recursion, recursion, etc.

Recursion is one of the most famous concepts in computer science because it’s quite fun!
In this article, I will explain recursion and its different types and show you some famous examples.
What is Recursion?
Recursion is when a function calls itself, but the input will typically change. So, as the function is calling itself, it’s known as a recursive function.
You are essentially breaking down the problem into more minor problems, which are solved independently but added together step by step.
Pretty much every recursive function can be written in a loop format, but the recursive framing is often much more elegant!
A Russian Doll can be considered a recursion, as each doll contains another doll, then that one contains another etc.
Recursion could technically go on forever, but there are often some stopping criteria that prevent this. Otherwise, the computer will quickly run out of memory!
In general, a recursive function has two things:
- Base Case — Terminating scenario that does not require recursion.
- Recursive Case — The actual recursion process.
Factorial
A common example is the factorial function:
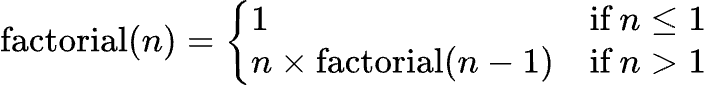
You can see how this is recursive because the factorial function is calling itself several times.
So, if we had n = 4, then the output would be 4*3*2*1 = 24. One can see how we are calling the factorial(n-1) process here.
Below is an example of the implementation of a recursive function for factorial. We have a base case for factorial(0) and factorial(1) as these return 1. Otherwise, we apply the recursive part.
def factorial(n):
# Base case: if n is 0 or 1, return 1
if n <= 1:
return 1
# Recursive case: multiply n by the factorial of n-1
else:
return n * factorial(n - 1)
This process is an example of one-branch recursion as we calling the function only a single time. The diagram below illustrates this.
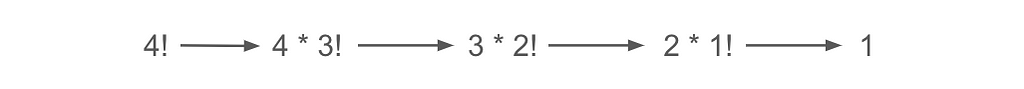
This function’s time complexity is O(n), as we call the factorial function n times.
The space complexity is also O(n), as we call the factorial function n times in memory.
Fibonacci Sequence
The Fibonacci sequence is a process where the following number is the sum of the previous two: 0, 1, 1, 2, 3, 5, 8, …
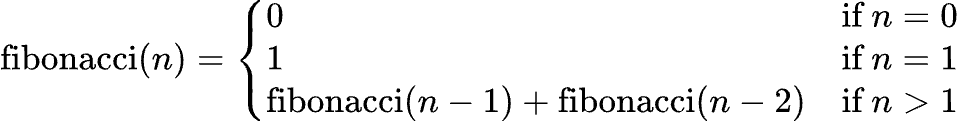
As we call the function twice, this is an example of a two-branch recursion. The function below illustrates this:
def fibonacci(n):
# Base cases: return 0 if n is 0, and 1 if n is 1
if n == 0:
return 0
elif n == 1:
return 1
# Recursive case: sum of the two previous Fibonacci numbers
else:
return fibonacci(n - 1) + fibonacci(n - 2)
Below is a diagram that illustrates this process:
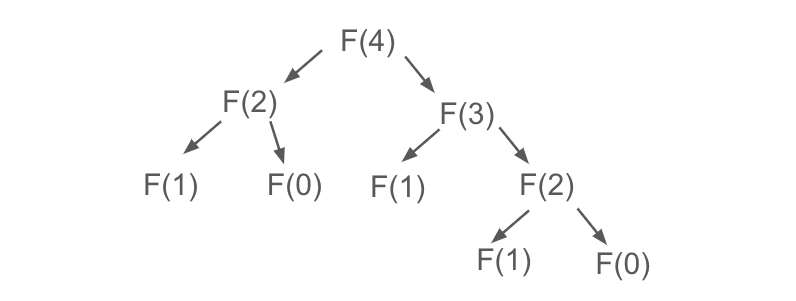
Each function needs to recursively call two functions constantly, so this is where we get the two branches.
The time complexity for two-branch recursion is slightly more complicated to calculate. However, you can see that as we go down the tree, the number of calculations doubles.
The total number of nodes in the tree is 2^n, so the time complexity is also O(2^n), as that’s the total number of function calls we need to do.
Recursion vs Iteration
As mentioned earlier, you don’t have to use recursion; you can achieve the same outcome using iteration. Below is an example iteration code for the factorial and Fibonacci sequences.
def factorial(n):
result = 1
for i in range(2, n + 1):
result *= i
return result
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
prev, curr = 0, 1
for _ in range(2, n + 1):
prev, curr = curr, prev + curr
return curr
So, the question begs, when should we use iteration vs recursion?
In general, iteration is actually more compute-efficient than recursion. However, recursion is a neater, more elegant implementation. So, it all really comes down to the individual scenario.
Summary & Further Thoughts
Recursion is a crucial computer science concept and is when a function calls itself with modified input until a base case, or termination condition, is met. There are different types of recursive functions, such as one-branch and two-branch. An example of a one-branch is the factorial function with a single recursive call. On the other hand, the Fibonacci sequence uses two-branch recursion, where each function call makes two more calls, resulting in exponential time complexity.
Another Thing!
I have a free newsletter, Dishing the Data, where I share weekly tips and advice as a practising data scientist. Plus, when you subscribe, you will get my FREE data science resume and a short PDF AI roadmap!
Dishing The Data | Egor Howell | Substack
Connect With Me!
- LinkedIn or Instagram.
- My YouTube Channel to learn technical data science and machine learning concepts!
- 👉 Book a 1:1 mentoring call
Recursion — Data Structures & Algorithms for Data Scientists was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Datascience in Towards Data Science on Medium https://ift.tt/1olXfqy
via IFTTT




