Marketing Mix Modeling (MMM): How to Avoid Biased Channel Estimates
Learn which variables you should and should not take into account in your model

“How will sales be impacted by an X Dollar investment in each marketing channel?” This is the causal question a Marketing-Mix-Model should answer in order to guide companies in deciding how to attribute their marketing channel budgets in the future. As we will see, the results to this question highly depend on which variables you account for: Omitting important variables, or including “wrong” variables in your model will introduce bias and lead to wrong causal estimates. This is a huge problem, as wrong causal estimates will eventually turn into bad marketing decisions and financial losses. In this article, I want to address this issue and give guidance on how to determine which variables should and should not be taken into account in your MMM, with the following structure:
- In 1. we will see why variable selection is so critical in Marketing-Mix-Models, by seeing how greatly channel estimates can vary depending on the set of variables you take into account in a simulated example.
- In 2. we will dive into potential sources of bias. You will understand which types of variables you should absolutely take into account, and which ones you should absolutely not take into account. This chapter is based on theory from standard works in the domain of causal inference by Judea Pearl [1][2] and on Matheus Facure’s very insightful website [3],
- In 3. we apply these learnings to our example with simulated data.
1. On the importance of variable selection in MMM’s
Let’s go through a simple example to showcase how critical variable selection is in MMMs. In order to keep things simple, and focus on the actual variable selection problem, we will stick to using simple linear regression. Keep in mind that the variable selection problem remains equally critical if using more complex MMM’s (e.g. Bayesian Models with Saturation & Carry-over effects).
Assume you work for the marketing department of an online sports shop, and your department has been advertising your platform through TV, Youtube and Instagram for 3 years. Now the time has come to estimate the contribution of each of these marketing channels on sales. You start by gathering weekly data on marketing channel spending, and company sales, and it looks as follows:
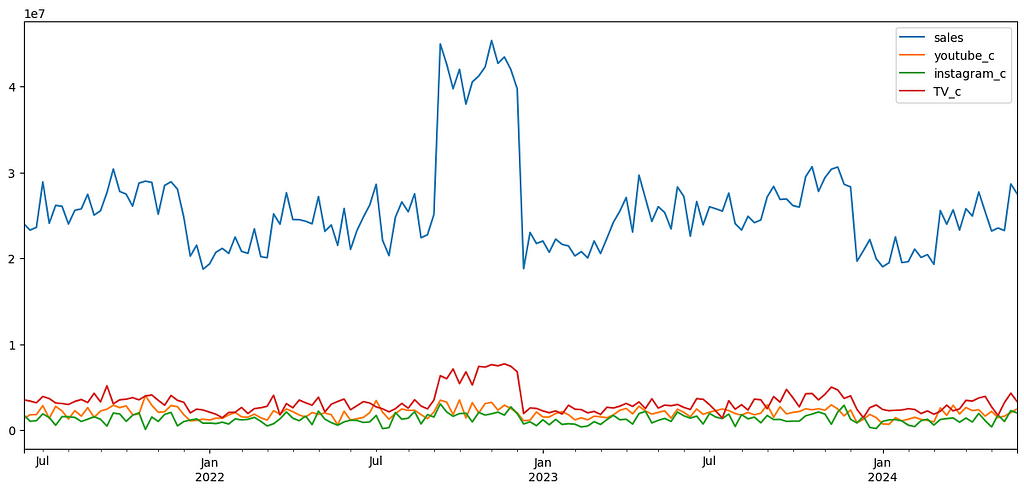
The most minimalistic approach for an MMM would be to fit the sales by a linear regression on the marketing channels:
However, you know that there are many additional variables that can have an impact on sales, and you wonder whether you should include them in your model. These are:
- Seasonal variables as you know that sales have a natural seasonal patterns
- A football world cup indicator variable as you know that sales go up during major sports events
- Price as you assume that sales vary strongly with price
- Website visits as you know that sales go up when there are more visits on your website
Given that you have the above data/variables, you decide to fit 5 different linear regression models, taking into account 5 different sets of variables:

Finally leading to the channels’ estimates represented below:
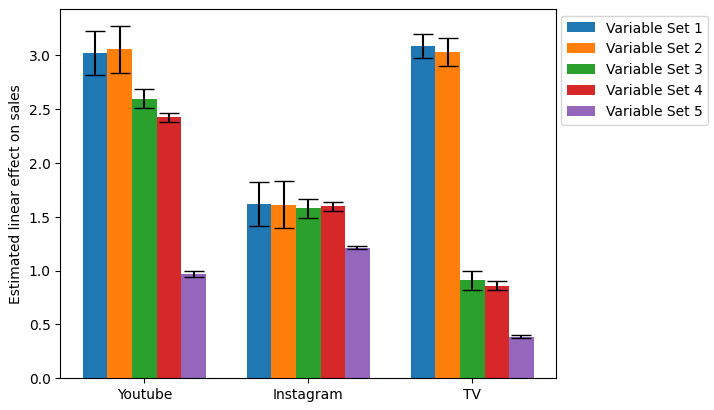
As you can see, the estimates for the different channels depend very strongly on the set of variables you take into account. This means that if you want to take model based marketing decisions, you will come to very different conclusions depending on which set of variables you choose. For instance:
What if you wanted to know whether to invest more on TV advertisement? According to Model 1, a 1$ investment on TV brings you about 3$ in sales, so you should invest more in it. In contrast, according to model 5 the generated sales will not even cover your advertising expenses (<0.5$ dollars sales for a 1$ expense) so you should cut down the TV spendings.
What if you wanted to know which channel has the biggest impact on sales, so that you can invest more in it? According to model 1, your most impactful channel is TV, according to model 2,3,4 it is YouTube, and according to Model 5 it is Instagram.
Bottomline — if you do not carefully select the variables in your MMM, you might as well take marketing decisions by rolling a dice. But don’t worry! Thanks to causal inference theory, there is a way to guide you in determining which variables you should take into account and which not! In the remainder of this article I will explain how, finally enabling you to know which out of the 5 sets of variables (if any) leads to accurate causal estimates.
Spoiler alert: Is “selecting the variables that lead to the most accurate predictions of sales” a good method? No! Remember, we are ultimately not interested in predicting sales, rather we want to determine the causal effect of marketing channels on sales. These are two very different things! As you will see, some variables that are very good predictors of sales, can lead to biased estimations of the causal effect of your marketing channels on sales.
2. Sources of Bias
Source 1: Omitting confounder variables
In order to achieve unbiasedness of your estimates, you should put a lot of thought into determining which variables are so-called confounder variables. These are variables you absolutely need to account for in your model, or you will have biased estimates. Let’s see why!
What is a confounder variable?
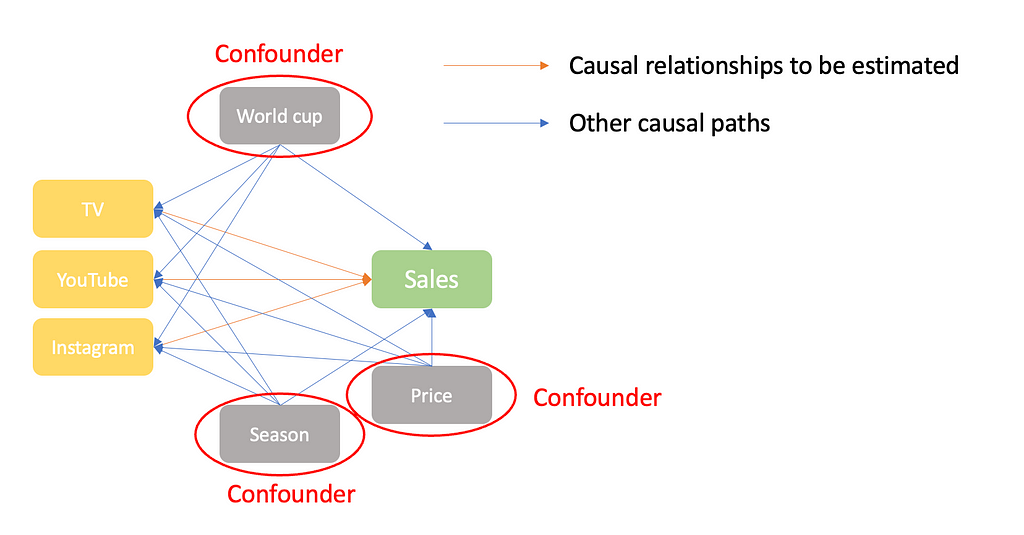
A confounder variable is a variable that has both a causal effect on the company sales, and on one or more of your marketing channels. For instance, in our online sports shop example, the variable “Football World Cup” is a confounder variable. Indeed, the company invests more in TV advertisement because of the World Cup, and the football World Cup leads to increased football jersey sales. Hence, leading to the following causal relationships:

Why do we need to account for confounder variables?
The problem if we do not account for this kind of confounding variable, is that our MMM “mixes-up” the effect of TV advertisement with the effect of the World Cup. Indeed, as the World Cup makes TV spendings and Sales both go up, it looks like the additional Sales generated by the World Cup are generated by the additional TV adds, when they are in fact largely due to the World Cup. This leads to a biased estimate of TV on sales. But luckily, this bias disappears if our model takes into account the “World Cup” confounder variable. Schematically, we can represent this as follows:
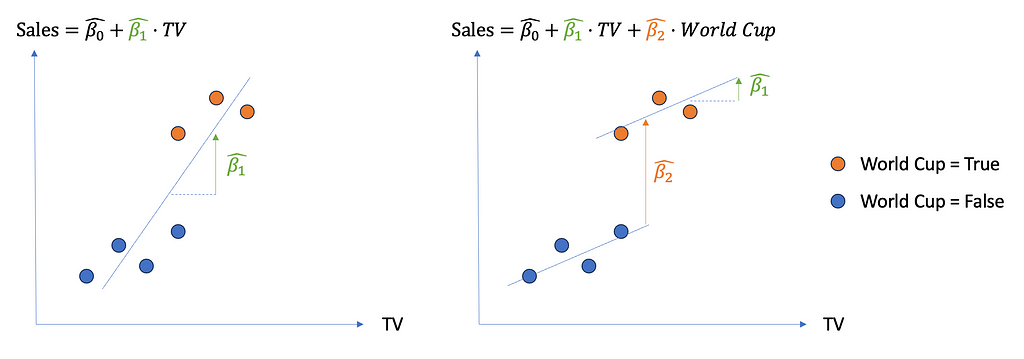
On the left, the model does not account for the effect of the world cup, and we can see that the estimated effect of TV on Sales is huge (large beta_1). This is due to the fact that the linear model confuses the causal effect of TV with the effect of the World Cup, which leads to a bias. On the right hand side, the estimated effect of TV is now substantially smaller, because the model rightly attributes the additional sales during the world cup period, to the World Cup itself (large beta_2, small beta_1).
How to identify confounder variables in MMMs?
In order to identify all confounders, you need to know all factors that have both a causal impact on your marketing channels, and on your company’s sales. A huge difficulty here is that the concept of causality is very theoretical, and only resides on assumptions! Hence, there is no way of knowing which variables have a causal impact just by looking at the data. You need to think conceptually, about which variables could impact sales and your marketing channel spendings. While it will be nearly impossible to list all factors that could have a causal impact on sales, as these are very diverse (e.g. inflation, state of economy, competition…), it should be much easier to identify the factors that influence your channel spendings, as these decisions / processes are made within your company, and can thus be investigated by talking to the relevant persons internally! In the end, if you identify the subset of factors that impact both channel spendings and sales, you’re good!
Examples of confounders in MMMs
- Seasonality: In most use-cases both sales and marketing budgets are very much impacted by the season of the year (e.g. sales & advertisement peak because of Christmas). In this case, seasonality is a confounder.
- Discounts: If your company launched a discount campaign that led to additional advertisement on the marketing channels, it is a confounder. Indeed, in this case, discounts impact both channel budgets and sales.
- Marketing competition: If your company reacts to an advertisement offensive of your competitor by investing more on marketing channels, this is a confounder. Indeed, the marketing campaign of your competitor has a (negative) causal impact on your sales, and it also leads your company to invest more on its own marketing channels.
- New product campaigns: Imagine your company launches a revolutionizing new product, that everybody wants to purchase, and it also decides to invest more in marketing channels in order to advertise that new product. Again, this is a confounder, as the new product will impact sales by itself, and also your marketing channel budgets.
As you have probably realized by now, this list could get very long, and depends very much on your company/use-case. There is no generic recipe that will give you all confounders. You need to become a detective, and watch out for them in your specific use-case, by understanding how marketing budgets are attributed.
What if there is a confounder you cannot measure?
In some cases, there will be confounder variables, for which you have no data, or that are simply not measurable. If these are strong confounders, you will also have strong biases, and you might consider dropping the MMM project entirely. Sometimes it is just better to have no estimates than to blindly trust wrong estimates.
We have now seen what goes wrong when we do not or cannot take into account confounder variables. Let’s now see what can go wrong when we take the wrong variables into account in our model.
Source 2: Including mediator variables
Oftentimes, we tend to think that “nothing can go wrong if we just control for one more variable”. But as will see shortly, this statement is false. Indeed, if you control for so-called mediator variables, the causal estimates for your marketing channels will be biased!
What is a mediator variable?
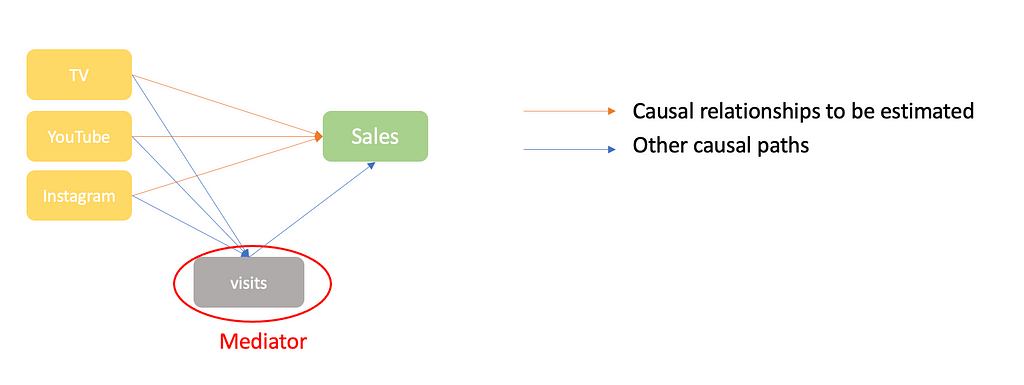
In a context where you want to measure the impact of TV advertisement on sales, a mediator variable is a variable through which TV indirectly impacts Sales. For instance, TV advertisement might impact sales indirectly by increasing the number of visitors to your online shop:

Why does accounting for mediators create bias?
If you do not take into account the mediator “visits”, your model’s estimate for the impact of TV on Sales will account both for the direct effect (TV → Sales) and the indirect effect (TV → Visits → Sales). This is what you want! In contrast, if you take into account the variable “visits”, your TV estimate will only account for the direct effect on sales (TV → Sales). The indirect effect (TV -> Visits -> Sales) will instead be captured by your model’s estimate for the impact of increased visits. Hence, your TV estimate does not account for the fact that TV increases sales through visits, leading to a bias of your causal estimate of TV on sales!
Let’s see this with equations! Assume the sales can be described by the following linear equation:

If you specify a linear regression model that takes into account both TV and visits, you will estimate the direct causal effect of TV on sales, but the indirect effect remains hidden through the variable “visits”:
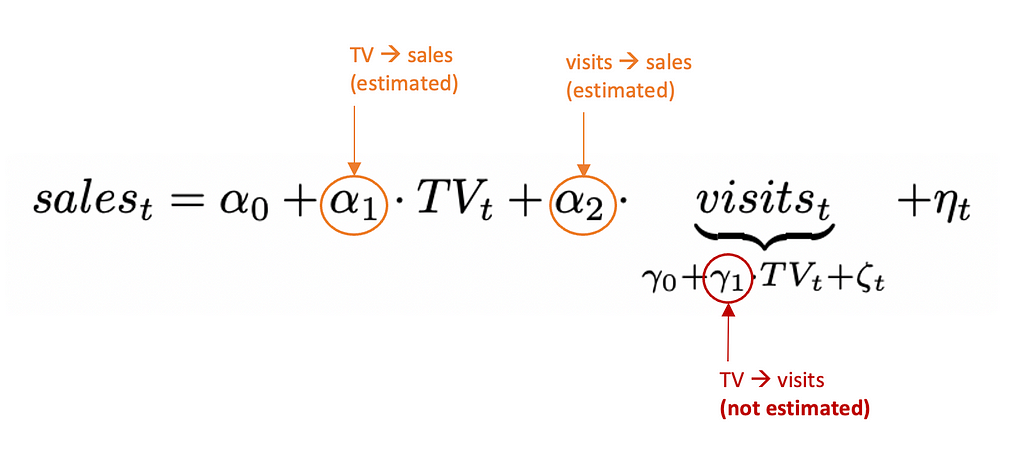
In contrast, if you do not take into account the variable “visits” in your linear model, you will correctly estimate the causal effect of TV to be the sum of its direct and indirect effect on sales:
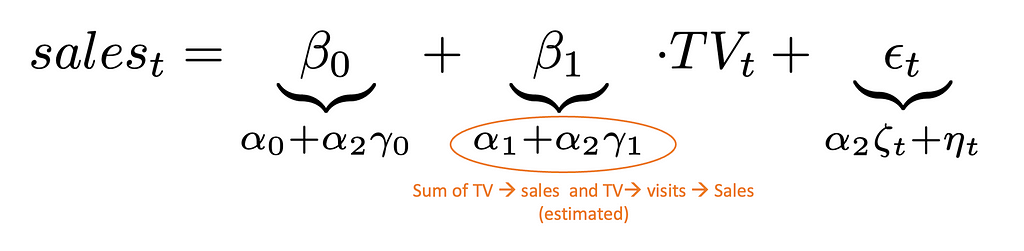
Challenges with mediators in MMMs
In most cases it is easy to avoid the mistake of taking into account a mediator variable in your MMM use-case. For each variable you plan to take into account, ask yourself whether one of your marketing channels have a causal impact on it. If yes, drop this variable! Easy. However, a problem arises when that mediator variable is actually also one of your marketing channels! This can actually happen, for instance, if you estimate the impact of your company’s paid search channel, along with the impact of your other marketing channels (e.g. TV). Indeed, advertising your product via TV might lead customers to search your product online, which will increase your paid search expenses. Hence the paid-search channel would be a mediator for the effect of TV on sales:

This case is challenging, as there is no way of getting an unbiased estimates for both TV and paid-search. Indeed, you only remain with the following two options:
- You drop the variable paid-search, so you obtain an unbiased estimate for TV. However, you do not get any estimate for your paid-search channel.
- You keep the variable paid-search, enabling you to get an unbiased causal estimate for paid-search. However, this leaves you with a biased estimate for TV.
Option 1 or 2 — Your choice to make!
Source 3: Including collider variables
Another type of variable that would introduce bias, if taken into account in your MMM are so-called collider variables.
What is a collider variable?
A collider variable for the effect of TV on sales is a variable that is causally impacted both by TV and by Sales:
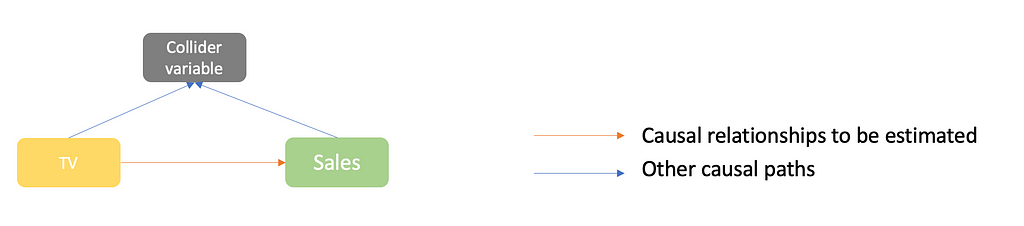
Examples of colliders in MMMs
One example for a collider variable in an MMM setting would be company profits. Indeed, a marketing channel (e.g. TV) impacts profits negatively through its costs, and profits are impacted positively by sales. Although it is possible to come up with such examples of collider variables in the context of MMM’s, it would be really uncommon for anyone to consider such a variable in the first place. For that reason, I will not dive deeper into why taking into account collider variables would lead to bias. If you are interested in more details, I invite you to have a look at [Mattheus Facure’ website]
3. Simulation results
Now that we know how to select the right variables for our MMM, let’s jump back to our initial example and determine which variables to select. First, let’s display how the data in our example was generated.
Simulated data:
The marketing budgets were specified as follows:
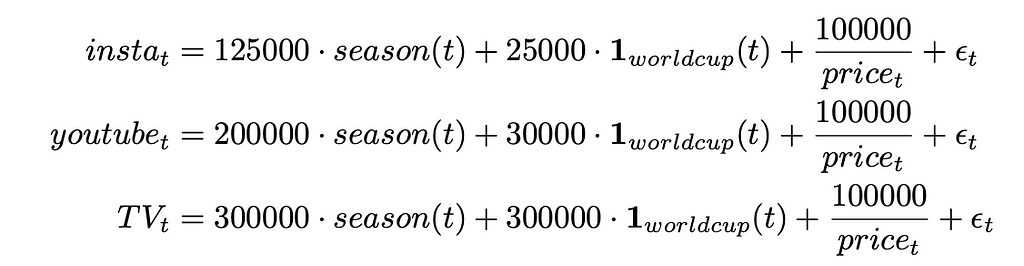
So in short, the three channels are causally impacted by the season, the world-cup and the price. The rest of the variation is random.
The sales amount on the website was specified as follows:
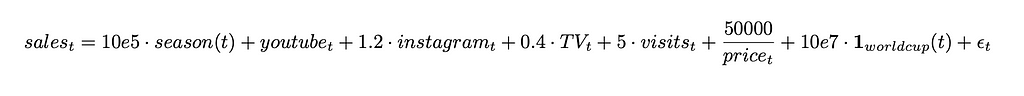
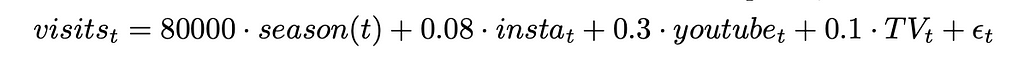
In short, the sales depend on the season, the budget in the marketing channels, the prices, the world-cup and the visits on the website. Note that the visits themselves depend on the marketing budgets and the season.
Now that we know the causal relationships between variables in the simulated data, we can determine which variables are confounders, mediators or colliders for the causal relationships to be estimated ( → Causal effect of marketing channels on sales).
Variable types:
As we can see in the formulas, the season, worldcup and price impact both the budget allocation to marketing channels and the sales. Hence, these 3 variables are confounders and should thus be accounted for in our MMM.
As we can see in the formulas, the variable visits is a mediator. Indeed, marketing channels causally impact visits and visits causally impact sales. Hence, this variable should not be accounted for in the model.
True causal effect:
From the equations that specify how we generated the simulated data, we can easily retrieve the true causal effect of the marketing channels.
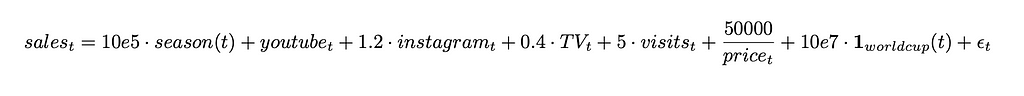
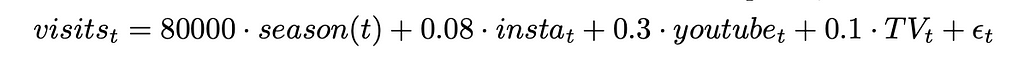
The true causal effect of a channel is composed of a direct effect on sales (channel → sales), and an indirect effect via the increase of visits (channel → visits → sales). For instance, a 1$ increase in the youtube channel directly increases sales by 1$ (resp. 1.2$ for instagram, and 0.4$ for TV), see the “sales” equation above. A 1$ incease on the youtube channel increases the number of visits by 0.3 (resp. 0.08 for instagram, and 0.1 for TV), see the “visits” equation. In turn each visit increases sales by 5$, see the “sales” equation. Leading to a total causal effect of youtube of 1 + 0.3*5 = 2.5$ (resp. 1.2 + 0.08*5 =1.6$ for instagram and 0.4+0.1*5 = 0.9$).
Estimated causal effects with different sets of variables:
We have now the knowledge of the true causal effects, and we can compare them with the estimations we would get when selecting different sets of variables (the sets specified in part 1).
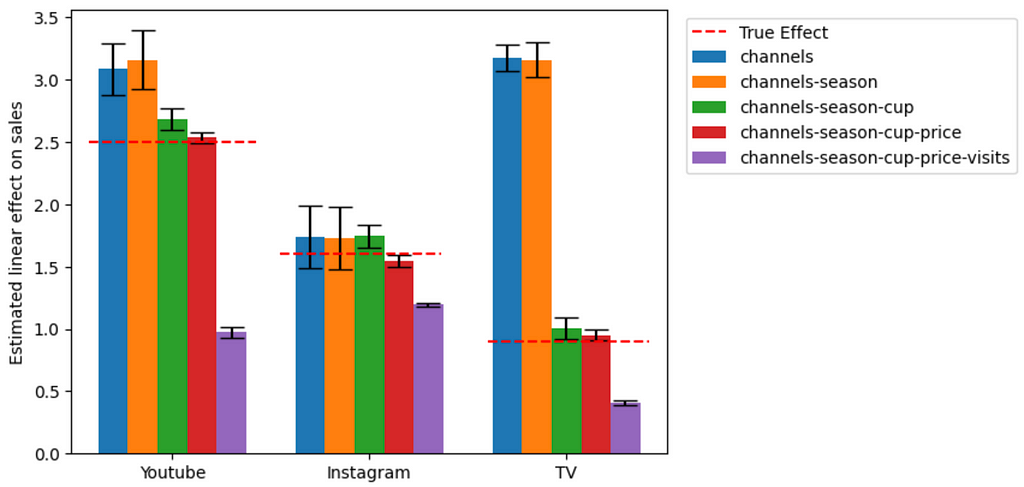
As we can see on the figure above, the true causal effect of the marketing channels on sales is only estimated correctly when all confounder variables are taken into account ( → Season, World Cup, Price) and the Mediators are not taken into account ( → Website visits). In contrast, one can observe large biases in the estimates of the marketing channels, when either the season, the world cup, or the price variables have been omitted. For instance, when all confounders are omitted, we estimate TV to have an impact three times higher than it actually has. We can also observe that taking into account the mediator variable leads to significant biases as well. For instance, we estimate the impact of the youtube channel less than half its real value when taking into account the variable visits into the MMM.
Conclusion
In conclusion, selecting the right set of variables is critical to obtaining unbiased causal estimates in Marketing Mix Modeling. As we could see in our example, not accounting for confounders or including variables such as mediators or colliders can significantly distort the results of your MMM, leading to misguided marketing decisions and potential financial losses. This should underline the importance of deeply think about the causal relationships involved between the variables you model. Once these are identified, you now know which variables you should take into account and which not to get unbiased channels stimates! For diving deeper, I highly recommend taking a read of the causal inference literature attached.
Note: Unless otherwise noted, all images and graphs are by the author.
[1] J. Pearl — The Book of Why: The New Science of Cause and Effect (2018)
[2] J. Pearl — Causality: Models, Reasoning, and Inference (2000)
[3] M. Facure — Causal Inference for the Brave and the True https://matheusfacure.github.io/python-causality-handbook/landing-page.html
Marketing Mix Modeling (MMM): How to Avoid Biased Channel Estimates was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Datascience in Towards Data Science on Medium https://ift.tt/wBIKkom
via IFTTT




