Datascience in Towards Data Science on Medium,

Trapped in the Net: Where is a Foundation Model for Graphs?

11/25/2024 Jesus Santana

|LLM|TRANSFORMER|FOUNDATION MODEL|GRAPH|NETWORK|

Disconnected from the other modalities graphs wait for their AI revolution: is it coming?

“If the foundation is solid, everything else will follow.” – Unknown

“The loftier the building, the deeper must the foundation be laid.” – Thomas à Kempis

Foundation models have changed artificial intelligence in recent years. A foundation model is a model trained with huge amounts of data (usually by unsupervised learning) that can be adapted to different tasks. Models such as BERT or GPT brought about a revolution in which one model could then be adapted for all tasks in a domain, simplifying AI access and reducing the need for data for a single task. We have foundation models for text and other modalities, but for modalities such as graphs and tabular data, we do not. In this paper we discuss why we do not have a foundation model for graphs and how we might get one, specifically, we will answer these questions:

• Why do we want a foundation model for graphs? Why do we not have one?
• Can we actually have a foundation model for graphs? and how?

Artificial intelligence is transforming our world, shaping how we live and work. Understanding how it works and its implications has never been more crucial. If you’re looking for simple, clear explanations of complex AI topics, you’re in the right place. Hit Follow or subscribe for free to stay updated with my latest stories and insights.

The quest for a graph foundation model

Foundation models have had a fundamental impact on the success of artificial intelligence in recent years. A foundation model is a large, pre-trained neural network that serves as a general-purpose model, capable of being fine-tuned for a wide range of downstream tasks. For example, large language models (LLMs) and wide CNNs have enabled great application development because of the ability of these models to be adapted to new tasks with little or no additional training.

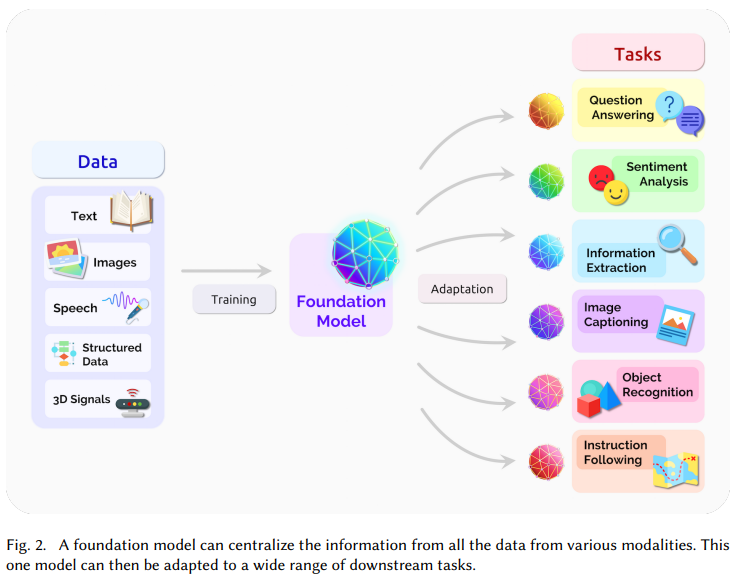
The significance of foundation models can be summarized by two words: emergence and homogenization. Emergence means that the behavior of a system is implicitly induced rather than explicitly constructed. Homogenization indicates the consolidation of methodologies for building machine learning systems across a wide range of applications — source: [2]

The success of these foundation models thus stems from these two main factors. The first means that we have a single model that (with or without adaptation) can be used for all tasks. This means that there must be some similarity between tasks and a general vocabulary that allows the transferability of patterns between tasks. The second aspect means that by training with enough data the model will also learn tasks for which it has not been explicitly trained.

• Emergent Abilities in AI: Are We Chasing a Myth?
• The Savant Syndrome: Is Pattern Recognition Equivalent to Intelligence?

For example, LLMs treat language tasks such as question-answering as word vocabulary, and they were all trained with a single task (next word prediction). So, trained on a huge amount of text, they learn a set of patterns and structures that can then be adapted to any other task.

This process has worked well with both text and images, and today it is the standard for these modes. The real world, however, is not only composed of these modes. For example, two types of modalities have not benefited from this revolution: tabular data and graph data.

In the former case, traditional machine learning methods are still considered superior in performance to deep learning. In the second case, there are deep learning models (Graph Neural Networks (GNNs)) that can be used with graph data. In both of these modalities, LLMs are not superior to methods previously in use.

• Tabula Rasa: Why Do Tree-Based Algorithms Outperform Neural Networks
• How the LLM Got Lost in the Network and Discovered Graph Reasoning

Why we do not have a graph foundation model?

In general, we can say that at present there is a lack of pre-trained Graph Foundation Models (GFMs) that could be used in the same way as LLMs. There have been attempts to use pre-trained GNNs as foundation models (adapting models already trained for other tasks) but they did not perform as well as hoped [1].

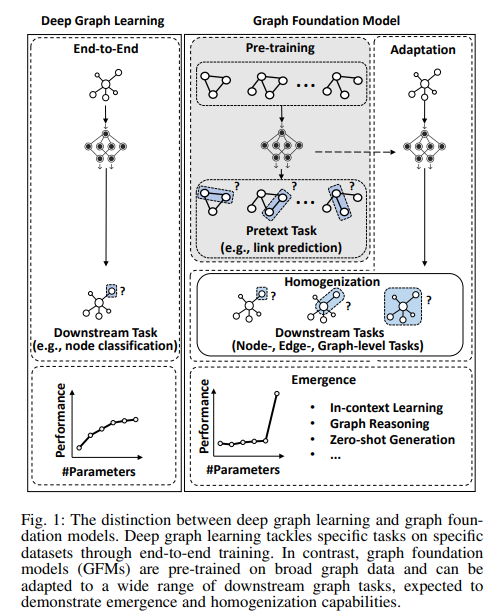
Therefore, the key challenges in achieving the GFM narrow down to how we can find the graph vocabulary, the basic transferable units underlying graphs to encode the invariance on graphs. — source: [5]

The problem with graphs is that although they are ubiquitous, they represent complex, non-Euclidean relationships among entities. The advantage of graphs is that they can represent countless structural patterns, but this makes it complex to construct a shared vocabulary [4–5]. For example, a model trained on social networks will not generalize to a molecular graph at all (nor do we know what vocabulary is shared).

So in summary, we are looking for a model that can be trained with a large amount of data in an unsupervised (pre-training step) manner and has two main features: Homogenization (The graph foundation model must be applicable to different graph tasks without having been explicitly trained for them) and Emergence (emergence of skills such as graph reasoning for which the model has not been trained). The main problem is that we have no idea what architecture to use and how to train such a model since we do not even know what a vocabulary that can encode transferable patterns shared among different graph tasks and domains.

Graph ML: A Gentle Introduction to Graphs

A common language for different graphs

There were some examples of looking for transferable patterns among the various graphs. Notable examples are the use of graphon theory. Graphs can be approximated by graphons representing their boundary behavior. Graphons serve as a mathematical tool to model the structural properties of graphs as they grow infinitely large. A graph in fact can be generated from a graphon (a graphon provides probabilistic rules for defining the connections between nodes, from which edges would then be sampled). So in theory, wide graphs could have graphons in common [6–8].

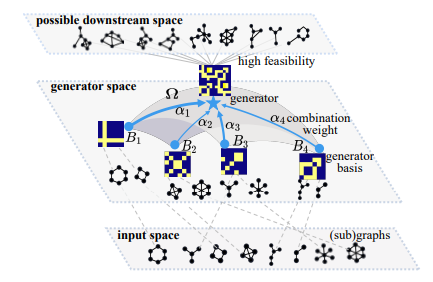
Despite the elegance of this theory, these models usually perform poorly with real-world datasets or in cross-domain settings. Other approaches have attempted to use subgraph structure instead [9–10]. According to these works, one can use localized subgraphs as transferable patterns within a graph vocabulary. These approaches seem to work better but are often time and memory-intensive. it is difficult to extract these subgraphs and GNNs fail to identify critical substructures in subgraphs, thus reducing the feasibility of the approach [11].

These approaches have failed because they do not work well with real-world graphs, do not capture local patterns, or are too expensive. So we want a system to get a vocabulary that has three characteristics:

• Efficiency. We don’t want it to be too expensive in terms of memory and computation.
• Expressiveness. It must be able to capture local patterns or motifs.
• Learnability. It must be learnable and be able to learn even elusive patterns.

Actually, GNNs under the hood learn local patterns and capture them in the embeddings they learn. Only these local patterns are not the subgraphs discussed above but subtrees called computational trees. In message-passing GNNs, for each node, we can construct a computational tree that contains its neighbors [12]. Computation trees have the properties they desire and are efficient to extract (automatically done by a GNN), they express local patterns and we can represent a graph as a multiset of them, and they are also capable of expressing elusive patterns.

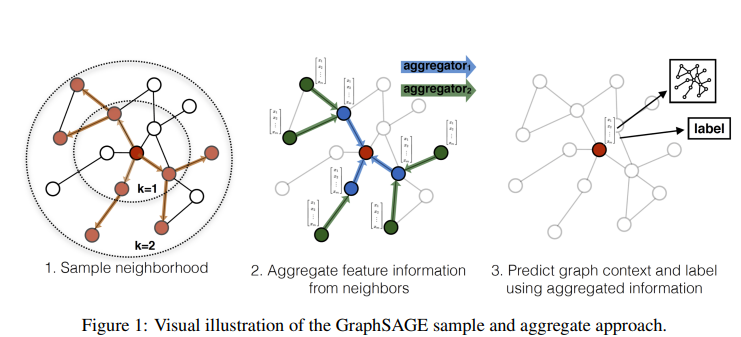
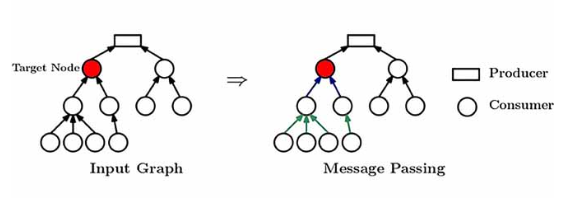
So we can treat computation trees as tokens within a graph vocabulary [1], this offers two advantages: preserving the essential information structure of the graph and you can use them for various tasks. In fact, GNNs can be used for various tasks (node-, link-, and graph-level tasks) but the learning process remains the same.

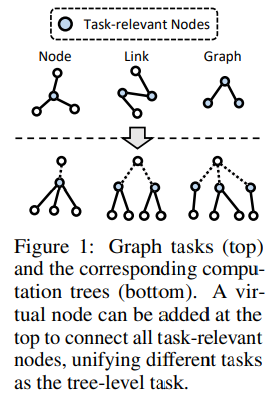
If two nodes share two similar computation trees (thus similar nodes) it means that they represent similar phenomena. If this occurs in two different graphs, we can transfer these patterns and thus fit our model. Also, similar computation trees should have similar embeddings, thus simplifying our work:

In particular, the distance between two computation trees is closely correlated to the similarity of their subtrees, where higher subtree similarity results in a closer distance. This suggests that computation trees with similar structures are likely to have similar embeddings, which enhances their transferability — source [1]

This can be easily verified. In fact, there is a correlation between computation tree similarity and transferability in real-world graphs. This means that we can transfer what a model learns.

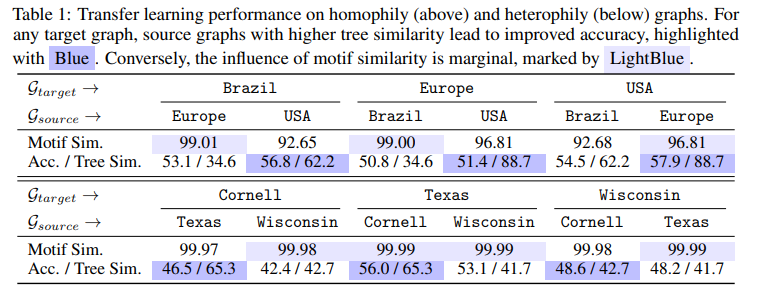
So in this approach [1] the model uses a cross-domain graph database using a generic task (computation tree reconstruction) that can be viewed similarly to that of an LLM learning to reconstruct a sequence. After that, the pre-trained model can be used for another graph. This model then learns an embedding of all these motifs and then uses this knowledge for other tasks.

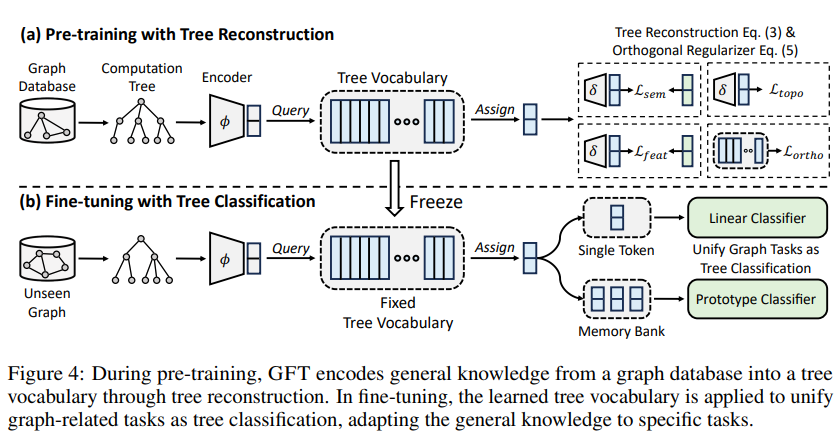
Now this model is still a message passing GNN and not a graph transformer. though we have all the elements we would need for our Graph Foundation Model. We have a set of tokens, we have a task to train with huge amounts of data, and we have an embedding. Moreover, the transformers are Graph Neural Networks [14]:

To make the connection more explicit, consider a sentence as a fully-connected graph, where each word is connected to every other word. Now, we can use a GNN to build features for each node (word) in the graph (sentence), which we can then perform NLP tasks with. Broadly, this is what Transformers are doing: they are GNNs with multi-head attention as the neighbourhood aggregation function. — [14]

The attention block can be seen as a GNN layer, especially looking at how it aggregates and processes information from neighboring nodes (the other tokens in the sequence). For each token or node, we conduct the representation update considering the influence of the other nodes or tokens. Similarly, in GNN and attention layers, we conduct a weighted sum of the influence of the other nodes and consider the context.

Parting thoughts

Foundation models and transfer learning were two paradigms that defined AI as we see it today. Foundation models allow for a single model that is trained with a large amount of generic data and then can be adapted to tasks where data is sparse with great performance. This versatility is one of the key reasons why AI has moved from a research product to a consumer product. Foundation models have become the standard because although they are expensive to train, it costs less to adapt them than to train a model for each task. In addition, they have reached state-of-the-art in all benchmarks and their performance improves with scale.

A Requiem for the Transformer?

Not all modes have enjoyed the benefits of a foundation model. This is the case with both tabular data and graphs. For tabular data, it is not yet clear whether deep learning is superior to traditional machine learning (XGBoost). For graphs, on the other hand, graph neural networks work very well. The lack of a vocabulary of transferable patterns has not allowed the creation of foundation models. Several studies that this is possible instead, and has been attempted in the past with less than stellar results. New ideas seem to show that we are finally close.

What do you think? How do you think foundation models for graphs can be achieved? Let me know in the comments

If you have found this interesting:

You can look for my other articles, and you can also connect or reach me on LinkedIn. Check this repository containing weekly updated ML & AI news. I am open to collaborations and projects and you can reach me on LinkedIn. You can also subscribe for free to get notified when I publish a new story.

Get an email whenever Salvatore Raieli publishes.

Here is the link to my GitHub repository, where I am collecting code and many resources related to machine learning, artificial intelligence, and more.

GitHub - SalvatoreRa/tutorial: Tutorials on machine learning, artificial intelligence, data science with math explanation and reusable code (in python and R)

or you may be interested in one of my recent articles:

• The Savant Syndrome: Is Pattern Recognition Equivalent to Intelligence?
• The Art of LLM Bonsai: How to Make Your LLM Small and Still Beautiful
• Traditional ML Still Reigns: Why LLMs Struggle in Clinical Prediction?
• Open the Artificial Brain: Sparse Autoencoders for LLM Inspection

Reference

Here is the list of the principal references I consulted to write this article, only the first name for an article is cited.

1. Wang, 2024, GFT: Graph Foundation Model with Transferable Tree Vocabulary, link
2. Bommasani, 2021, On the opportunities and risks of foundation models, link
3. Zhou, 2023, A Comprehensive Survey on Pretrained Foundation Models: A History from BERT to ChatGPT, link
4. Liu, 2024, Towards Graph Foundation Models: A Survey and Beyond, link
5. Mao, 2024, Position: Graph Foundation Models are Already Here, link
6. Cao, 2023, When to Pre-Train Graph Neural Networks? From Data Generation Perspective! link
7. Ruiz, 2020, Graphon Neural Networks and the Transferability of Graph Neural Networks, link
8. levie, 2019, Transferability of Spectral Graph Convolutional Neural Networks, link
9. Zhu, 2020, Transfer Learning of Graph Neural Networks with Ego-graph Information Maximization, link
10. Qiu, 2020, GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training, link
11. Zhang, 2024, Beyond Weisfeiler-Lehman: A Quantitative Framework for GNN Expressiveness, link
12. Hamilton, 2017, Inductive Representation Learning on Large Graphs, link
13. Hou, 2022, A Graph Neural Network Approach for Caching Performance Optimization in NDN Networks, link
14. Joshi, 2020, Transformers are Graph Neural Networks, link

---

Trapped in the Net: Where is a Foundation Model for Graphs? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

from Datascience in Towards Data Science on Medium https://ift.tt/2WwBSJP
via IFTTT