Water Cooler Small Talk: Why Does the Monty Hall Problem Still Bother Us?
STATISTICS
A look at the counterintuitive mathematics of game show puzzles

Water cooler small talk is a special kind of small talk, typically observed in office spaces around a water cooler. There, employees frequently share all kinds of corporate gossip, myths, and legends, inaccurate scientific opinions, indiscreet personal anecdotes, or outright lies. Anything goes. So, in my Water Cooler Small Talk posts, I discuss strange and usually scientifically invalid opinions I have overheard in the office that have literally left me speechless.
Here’s the water cooler opinion of today’s post:
‘-In a game show, you are given a choice among three doors: one door hides a car and the other two doors hide goats. You chose one of the doors, then the host reveals a goat behind one of the other doors, and gives you the option to swap the door you originally chose for the other remaining one. Should you swap?
-No, I will keep the door I initially chose. The chances are 50–50 either way.’
🚗🚪🐐🤪
If you didn’t recognize it already this is the famous Monty Hall problem. Spoiler alert, the chances are not 50–50; there is a 1/3 chance for the initially chosen door to reveal the car, and a 2/3 chance for the other doors, thus, the best strategy is to always swap the initial door. Crazy, right? As most of statistics, the Monty Hall problem is completely counterintuitive, even absurd, and never fails to make some jaws drop. In defense of my office coworkers, Paul Erdős, one of the most prolific mathematicians of the 20th century, remained unconvinced of these probabilities until he saw a relative simulation. In fact, most people get this wrong, unless they are already familiar with the puzzle.
🍨DataCream is a newsletter offering data-driven articles and perspectives on data, tech, AI, and ML. If you are interested in these topics subscribe here.
The Monty Hall problem
The Monty Hall problem is a probability puzzle. It was originally introduced to the audiences in the American television game show Let’s Make a Deal, and it’s named after the show’s original host, Monty Hall (duh!).

Here is what happens in the Monty Hall problem:
- There are three closed doors; behind one of the doors there’s a shiny new car 🚗; behind each of the other two doors there is a goat 🐐🐐
- You — the contestant — choses one of the three doors, say Door #1, hoping there is a car behind it.
- Then, the host reveals a goat behind one of the remaining two doors that you didn’t pick. For example, they open Door #3 revealing a goat.
- And finally, you are offered with a choice: Keep the door you initially chose, or swap it with the other remaining closed door.
So, what would you do? Does it matter? Is it 50–50?
Intuitively, we are inclined to believe that the chances are 50–50. After all, there are two doors left, one with a car and one with a goat. It should be 50–50, shouldn’t it?
No! 😠
When you initially choose Door #1, your chances of picking the car are 1/3. That means the probability that the car is behind one of the other two doors is 2/3. When the host reveals a goat behind Door #3, he doesn’t change the fact that the combined probability of Doors #2 and #3 hiding the car is still 2/3. By eliminating Door #3 that 2/3 probability is ‘redistributed’ entirely to Door #2. In this way, switching doors effectively gives you two chances out of three, while sticking with your original door leaves you with just one chance out of three.
Still not convinced? Let’s try to look at it from a different angle. In the initial choice among the three doors, the probabilities are as following:
- 1/3 probability to choose the car
- 2/3 probability to choose a goat
In other words, by always swapping the initially selected door, there is a 1/3 probability that we are getting rid of a car, and a 2/3 probability that we are getting rid of a goat.
Looking Behind the Doors
We can easily put together the respective simulation in Python. The three doors are illustrated as a list with 1 representing the car, and 0 representing the goats. Initially, the contestant randomly chooses a door, and then the host opens another door revealing a goat. The switch parameter indicates if the contestants sticks with their initial choice or switches to the other remaining door. And finally, given the switch we check if the contestant won. This process is repeated num_trials times, and in this way a winning percentage for each strategy (that is, sticking or switching) is calculated.
import random
def monty_hall_simulation(num_trials, switch):
wins = 0
for _ in range(num_trials):
# Place the car behind one of the three doors
doors = [0, 0, 0]
car_position = random.randint(0, 2)
doors[car_position] = 1 # 1 represents the car, 0 represents a goat
# Contestant makes an initial choice
contestant_choice = random.randint(0, 2)
# Host opens a door with a goat (not the contestant's choice or the car)
possible_doors_to_open = [
i for i in range(3) if i != contestant_choice and doors[i] == 0
]
door_opened_by_host = random.choice(possible_doors_to_open)
if switch:
# Contestant switches to the remaining unopened door
contestant_choice = [i for i in range(3) if i != contestant_choice and i != door_opened_by_host][0]
# Check if the contestant's choice has the car
if doors[contestant_choice] == 1:
wins += 1
return (wins / num_trials) * 100
# Parameters
num_trials = 10000
switch_strategy = monty_hall_simulation(num_trials, switch=True)
stick_strategy = monty_hall_simulation(num_trials, switch=False)
print(f"Win rate when switching: {switch_strategy:.2f}%")
print(f"Win rate when sticking: {stick_strategy:.2f}%")

See? Not 50–50. 🤷♀️
We can also visualize the simulation results for various numbers of trials, in comparison to the nominal probabilities:
import matplotlib.pyplot as plt
# Run simulations for both strategies over increasing number of trials
trial_counts = [100, 500, 1000, 5000, 10000, 50000]
switch_win_rates = []
stick_win_rates = []
for trials in trial_counts:
switch_win_rates.append(monty_hall_simulation(trials, switch=True))
stick_win_rates.append(monty_hall_simulation(trials, switch=False))
# Plot the results
plt.figure(figsize=(10, 6))
plt.plot(trial_counts, switch_win_rates, label='Switch Strategy', marker='o')
plt.plot(trial_counts, stick_win_rates, label='Stick Strategy', marker='o')
plt.axhline(66.67, color='blue', linestyle='--', label='Theoretical Switch Win Rate (66.67%)')
plt.axhline(33.33, color='orange', linestyle='--', label='Theoretical Stick Win Rate (33.33%)')
plt.title('Monty Hall Problem Simulation')
plt.xlabel('Number of Trials')
plt.ylabel('Win Rate (%)')
plt.legend()
plt.grid(True)
plt.show()
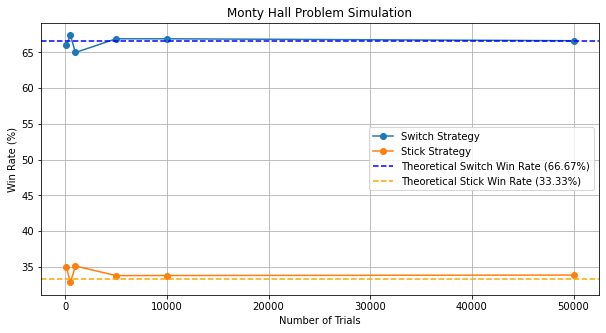
Thus, a player who keeps the initially chosen door wins 1/3 of the times, whereas, a player who swaps the initially chosen door wins 2/3 of the times.
What if there were more doors?
The mathematics behind the Monty Hall problem hold irrespectively of the number of choices in the game. In fact, the more the choices that are involved in the game, the greater the advantage of switching after the choices are narrowed down.
More specifically, if there were more doors, say N, then the probability of our initial choice being correct would be:

Additionally, the probability of the car being behind one of the other doors would be:
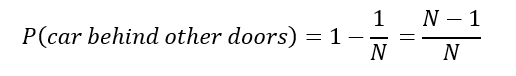
If the host opens, say p, incorrect doors and then offers the contestant the opportunity to switch with a randomly picked door out of the remaining ones, then we can calculate the winning probability of the new, switched door. That would be the probability of a specific door out of the remaining (N — p — 1) doors to contain the car, given that the car is behind some of the N initial doors. In other words, the dependent probability:
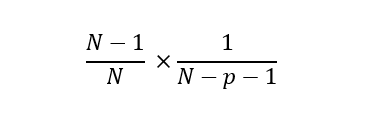
… which is always larger than 1/N. Thus, it makes sense to switch the initially chosen door, even if the host has only opened one extra door!
As the host eliminates all incorrect doors except one, the probability of the car being behind that remaining door also becomes:
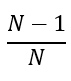
… which gets larger, as the number of doors increases. I believe that visualizing the game with a large number of N choices (instead of just 3 doors in the original game), makes it easier to intuitively grasp the statistics of it. We may get confused thinking the 2 out of 3 remaining doors of the Monty Hall problem, thinking the chances may be 50–50. Nonetheless, if we think about eliminating 998 out of 1,000 doors, it becomes much clearer that it is highly unlikely that we chose the correct 1 out of 1,000 doors in our first try. Therefore, it makes sense to swap it.
A great example of this is the Deal or No Deal game show, which although not identical to the Monty Hall game, mirrors this logic to a large extent. In particular, in Deal or No Deal:
- There are 26 briefcases containing various money prizes ranging for minor amounts to 1 million USD.
- The contestant selects one briefcase at the start of the game, hoping it contains the largest prize.
- As the game progresses, the contestant randomly opens and eliminates the other briefcases and respective money prizes, narrowing down the choices.
- At certain points throughout the game, the host (or more precisely the banker) offers the contestant a deal to exchange their briefcase for money or another briefcase.
The switching logic of Monty Hall applies here too. The briefcase that is initially chosen has a 1/26 chance of containing the highest prize — which is rather low. Eliminating the other briefcases as the game progresses doesn’t change the fact that it is unlikely that we chose the best briefcase on the first try. As fewer briefcases remain, switching (or taking a deal) offers a statistically better chance of winning a large prize.
On my mind
Much like the Birthday Paradox, the Monty Hall problem is a veridical paradox — even if mathematically proven and correct, is highly counterintuitive and appears to be false at first glance. We can see the evidence laid out in front of us — logical proofs and numerical simulations all lead to the same conclusion. Switching doors is the optimal strategy. And yet, we can’t really wrap our heads around it — for many of us, it might feel counterintuitive and just wrong.
We struggle to let go of the instinct that once the host opens a door, leaving two options, the chances should be 50–50. The equal probability assumption is deeply rooted in our intuition. It’s like it’s imprinted on our brains, that once presented with two options of anything — two sides of a coin, red/black roulette, True/False questions , anything really —it’s automatically equivalent with a 50–50 chance. Even when the numbers tell us otherwise, we find it hard to bypass our troubled statistical intuition and really pay attention to think logically. Ultimately, we might accept the outcome intellectually, but emotionally, something may still bother us.
Interestingly, this resistance to accepting counterintuitive probabilities seems to be a uniquely human limitation. An impressive 2011 study found that pigeons, unlike humans, are remarkably good at learning to switch their choice after playing several rounds of the Monty Hall game. Through trial and error, the pigeons observed that switching led to better outcomes and quickly adapted their behavior. A rather humbling reminder that overthinking, flawed intuition and cognitive biases, can get in the way of making the optimal decisions.

✨Thank you for reading!✨
Loved this post?
💌 Join me on Substack or LinkedIn ☕, or Buy me a coffee!
or, take a look at my other water cooler small talks:
- Water Cooler Small Talk: The Birthday Paradox 🎂🎉
- Water Cooler Small Talk: Gambler’s Fallacy and Ruin
Water Cooler Small Talk: Why Does the Monty Hall Problem Still Bother Us? 🐐🚗 was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Datascience in Towards Data Science on Medium https://ift.tt/BzKi0HP
via IFTTT




